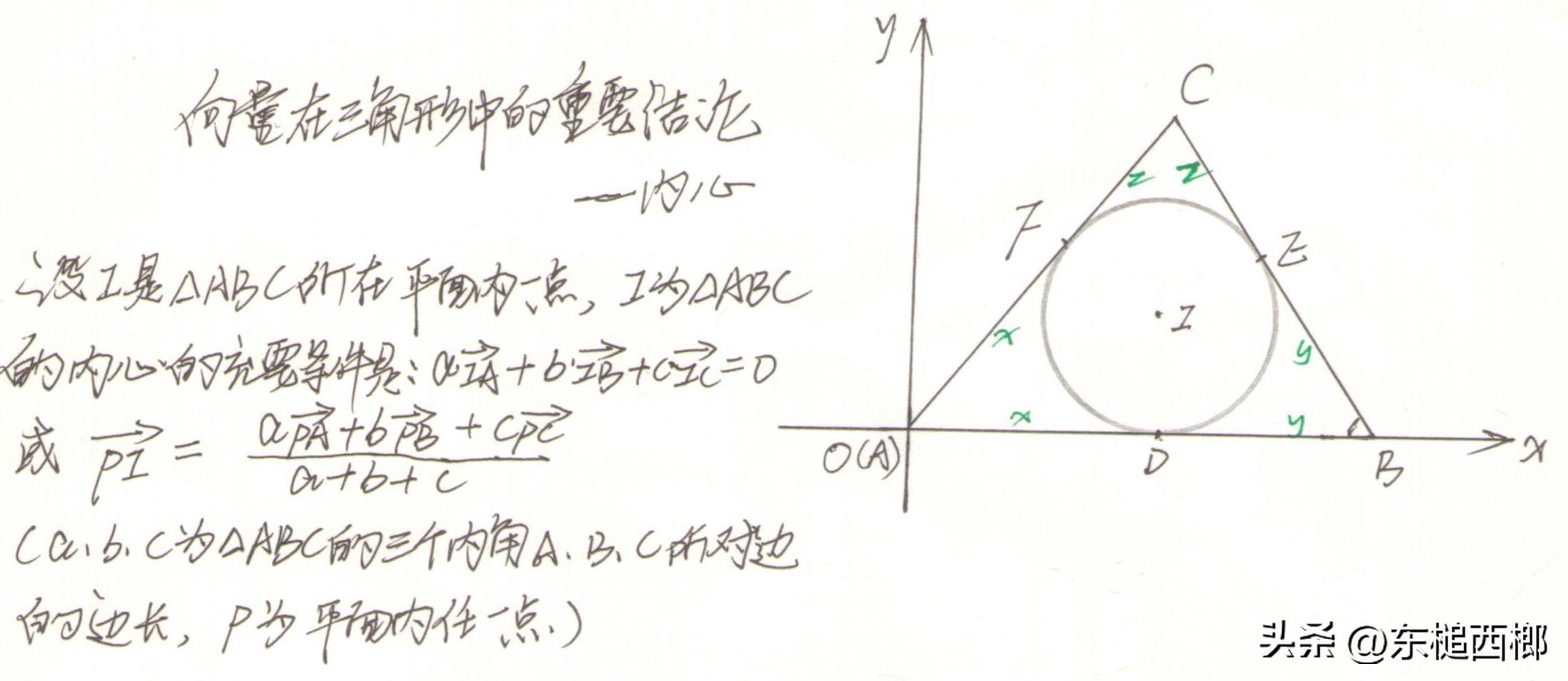
如上图所示,设I是三角形ABC所在平面内的一点,
点I为三角形内心的充要条件是aIA+bIB+cIC=0或PI=aPA+bPB+cPC/a+b+c.(a,b,c是三角形ABC的三个内角A,B,C所对边的边长,P为平面上任意一点,黑体表示向量)
证明过程如下图所示,第一步建立平面直角坐标系,第二步将A、B、C、I四点的坐标表示出来,第三步将向量IA,IB,IC用a,b,c和角B表示出来,第四步,进行向量坐标运算,运算过程有点繁琐。

知识回顾,三角形内心的性质。如下图所示:
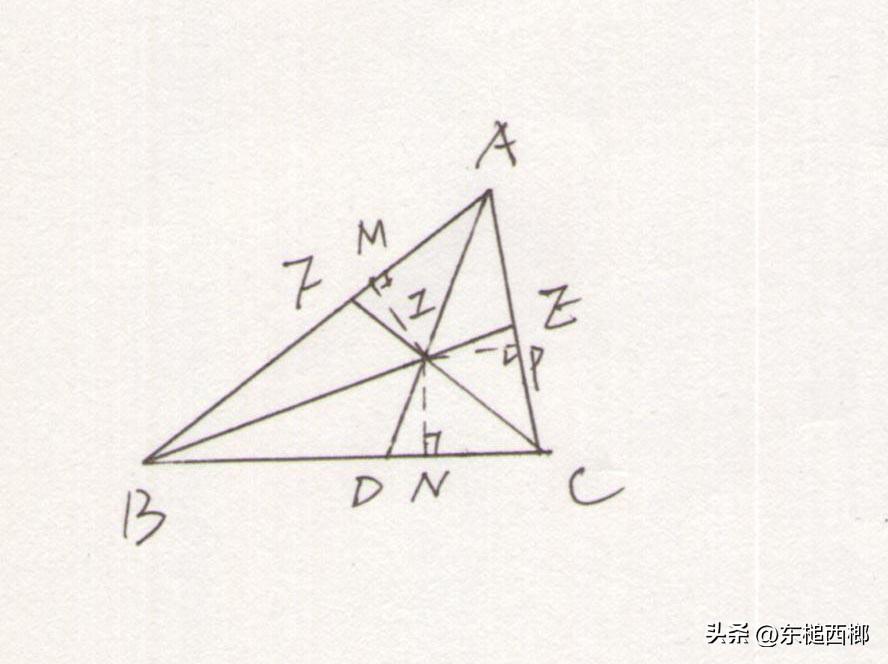
在三角形ABC中,AD、BE、CF分别是三内角的平分线。记AD与BE的交点为I,过I分别作AB、BC、CA三边的垂线,垂足分别为M,N,P。
根据角平分线的性质,IP=IM,IM=IN,所以IP=IN。
因此,点I在角C的平分线上,即CF通过点I。
即三条内角平分线交于一点,这交点叫做三角形的内心。
内心与各顶点的连线平分各角,内心到三角形三边的距离相等,内心也是三角形内切圆的圆心。