一,四则运算数独
1,四则运算数独是升级版的数独,是在数独规则的基础上加入了加减乘除四则运算,解题时需要更多的运算试算,比数独更有挑战性,更能锻炼思维。
2,四则运算数独,简称“算独”,又称聪明方格,聪明格,算独,肯肯数独, Kendoku,Kenken。
3,算独,被认为是继数独(Sudoku)之后最具人气的一种算术游戏,是一项可以开发大脑潜能、提高集中力层次的益智游戏。
二,3×3四则算独规则
1,每一行、每一列均含数字1~3,且不重复。
2,左上角的“数字+”代表粗框内所填数字之和。
3,左上角的“数字-”代表粗框内所填数字之差。
4,左上角的“数字×”代表粗框内所填数字之积。
5,左上角的“数字÷”代表粗框内所填数字之商。
三,唯一框格法
当粗框只是一个单元格时,左上角的数字就是此格正确的填数。

r2c3=3
四,和唯一组合法
〔一〕和为3
因为:3=1+2
所以:3+=(12)
〔二〕和为4
因为:4=1+3
所以:4+=(13)
〔三〕和为5
因为:5=2+3
所以:5+=(23)
五,差组合法
〔一〕差为1
因为:2-1=1,3-2=1
所以:1-={12,23}
〔二〕差为2
因为:3-1=2
所以:2-=(13)
六,积唯一组合法
〔一〕积值为2
因为1×2=2
所以2×=(12)
〔二〕积值为3
因为1×3=3
所以3×=(13)
〔三〕积值为6
因为2×3=6
所以6×=(23)
七,商唯一组合法
〔一〕商值为2
因为2÷1=2
所以2÷=(12)
〔二〕商值为3
因为3÷1=2
所以3÷=(13)
八,排除法
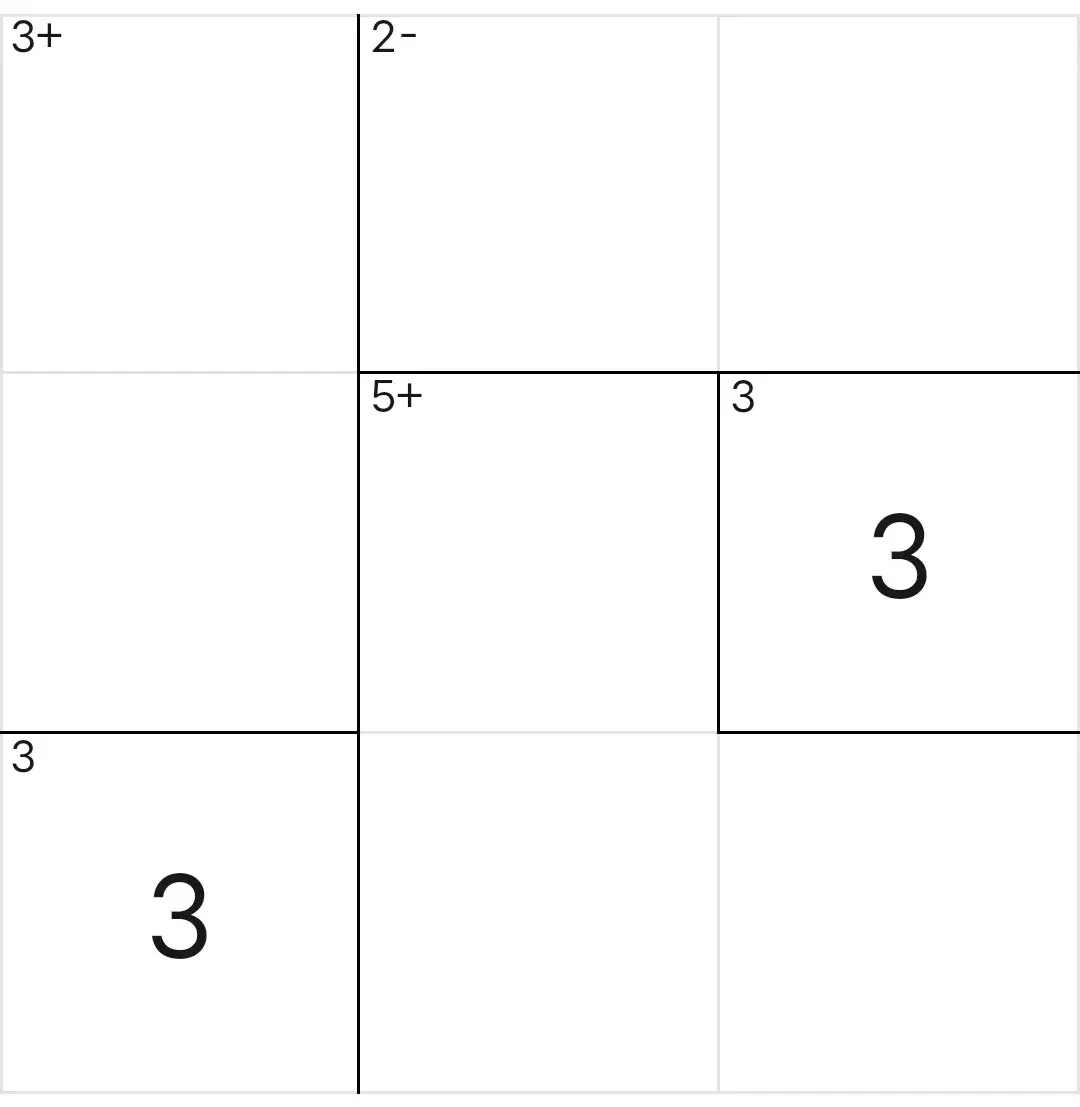
利用数字3对第一行作排除
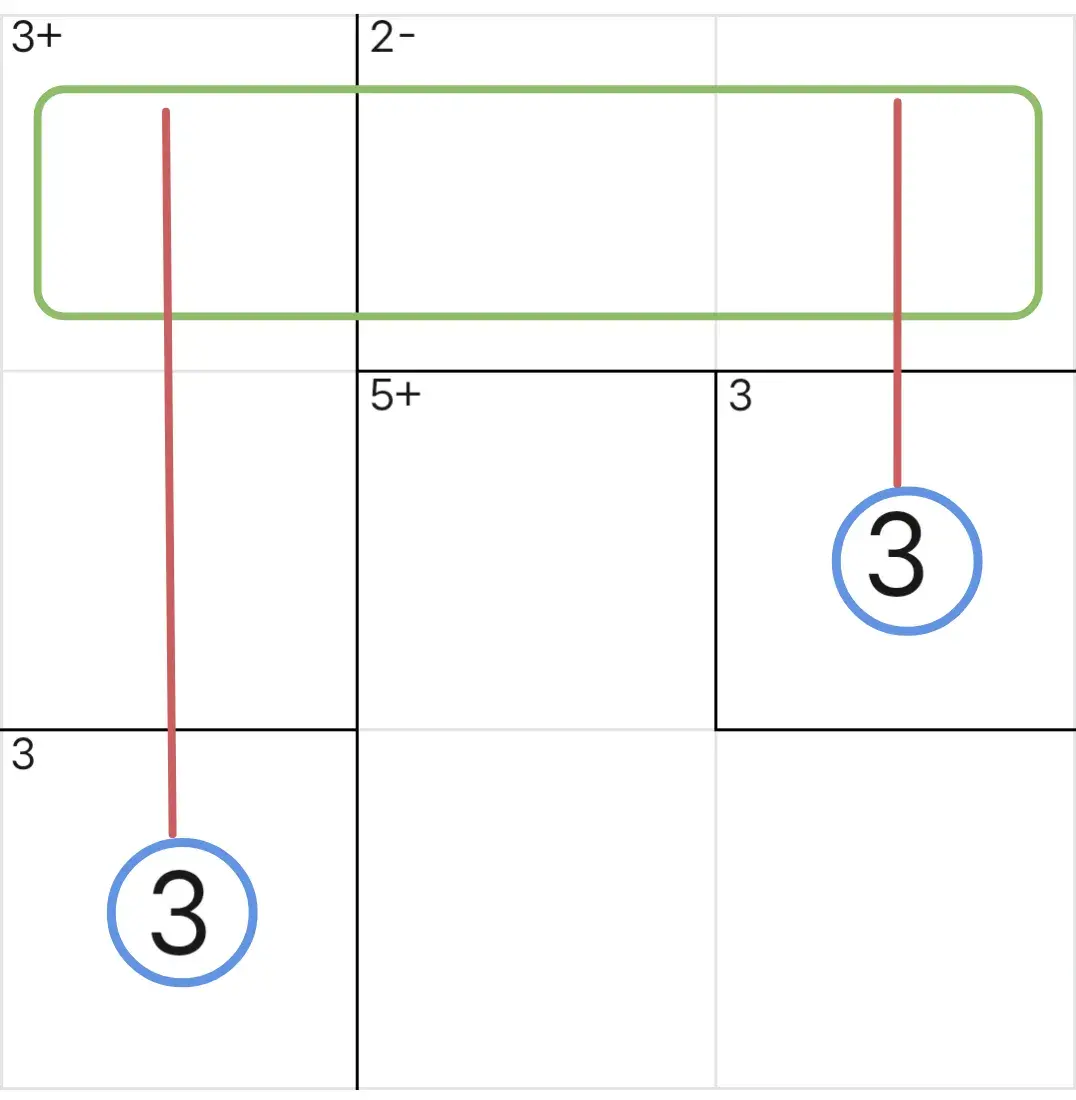
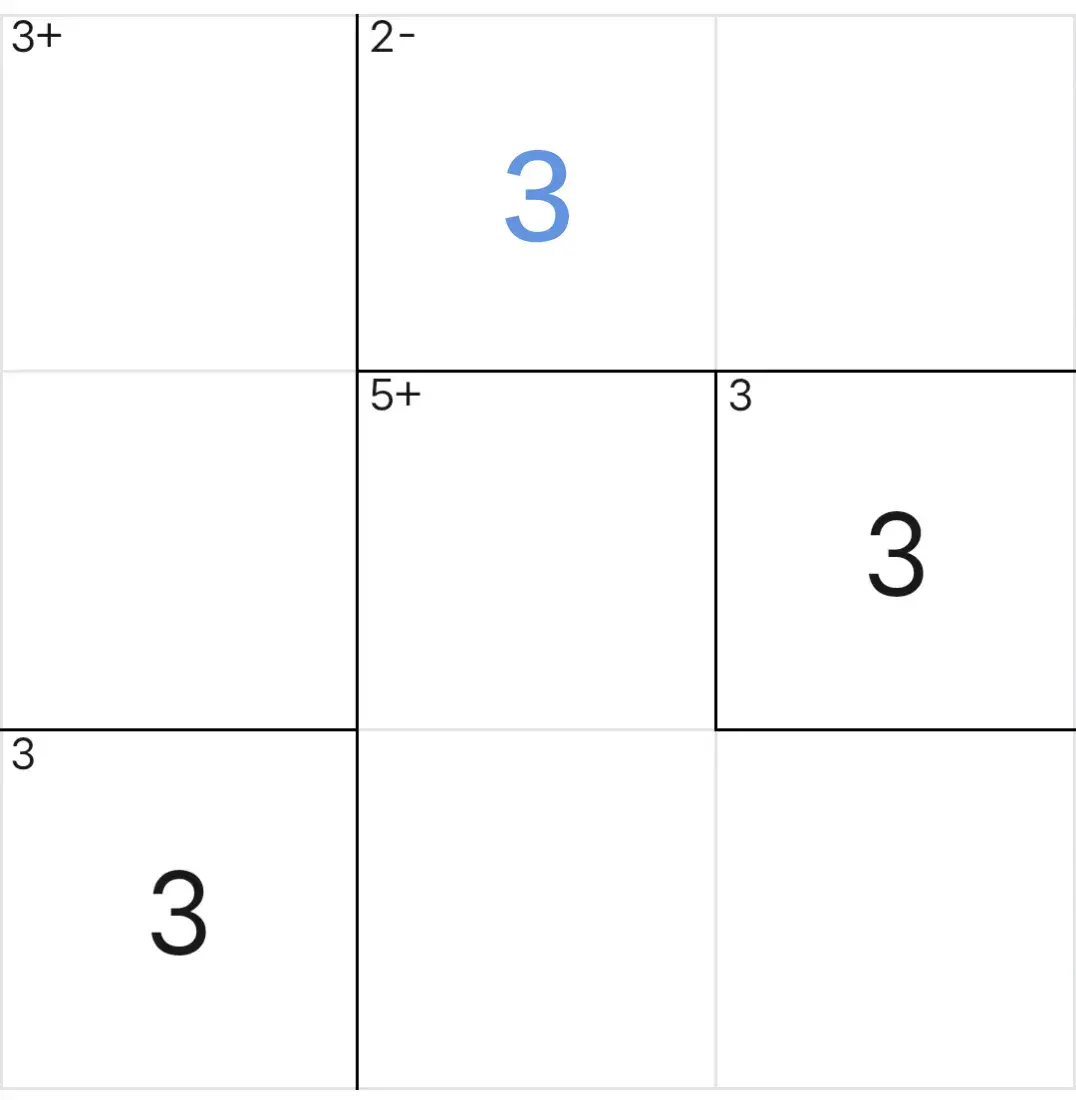
r1c2=3
九,区域对比法

〔一〕观察第三行
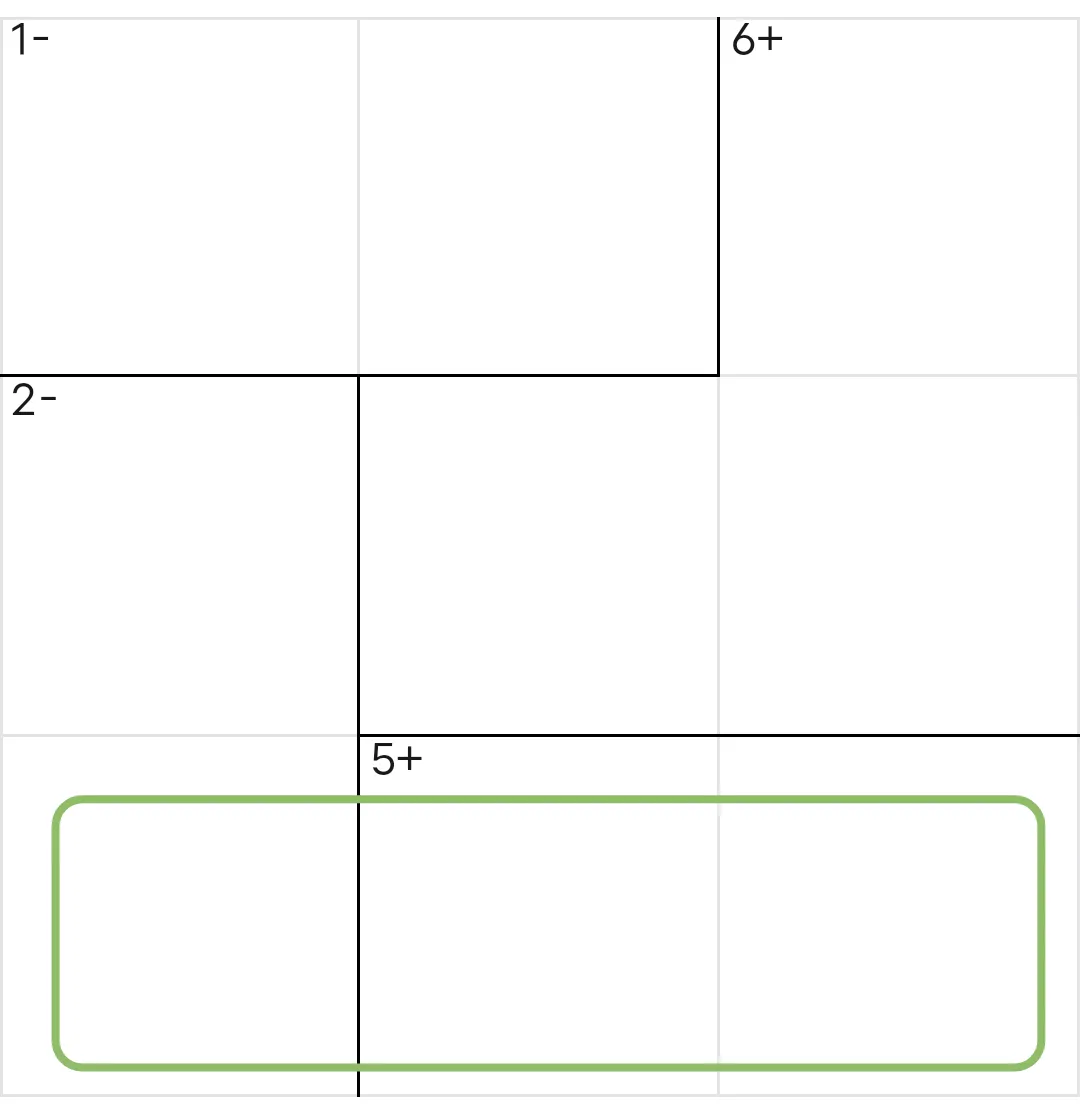
存在和为5的两格粗框
〔二〕根据数独规则:每一行、每一列均含数字1~3
所以第三行中必含数字123
因此,本行的数字和是:1+2+3=6
〔三〕计算差值
行区与框区对比:只剩下唯一空格r3c1
行和与框和之差:6-5=1

所以,r3c1=1
〔四〕观察第二行
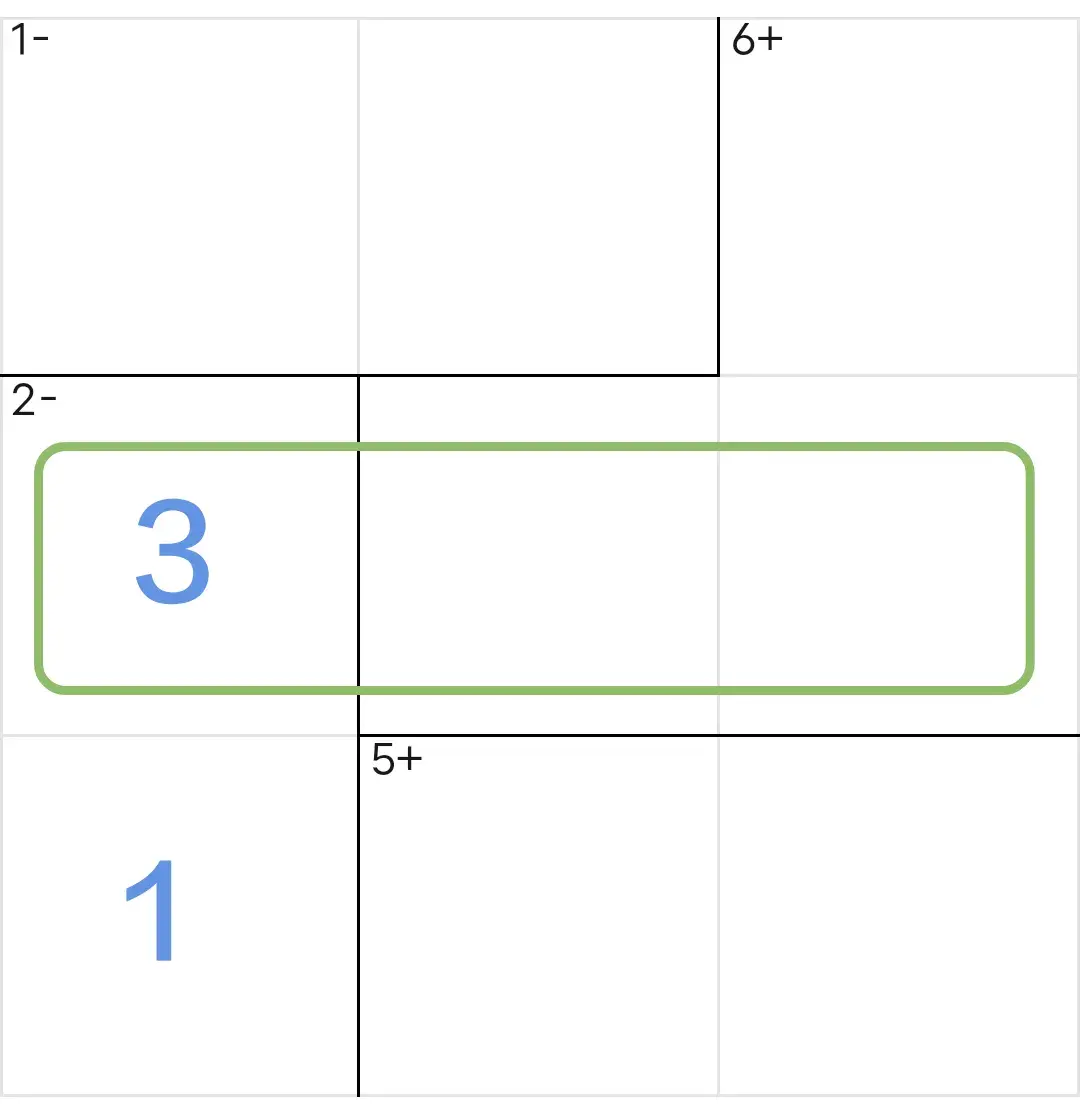
存在一个和值为6的粗框
〔五〕和值为6的粗框加上数字3的格r2c1,构成一个新的大区
大区的和值是:6+3=9
〔六〕计算差值
大区减去第二行之后:只剩下唯一空格r1c3
大区和与行和之差:9-6=3
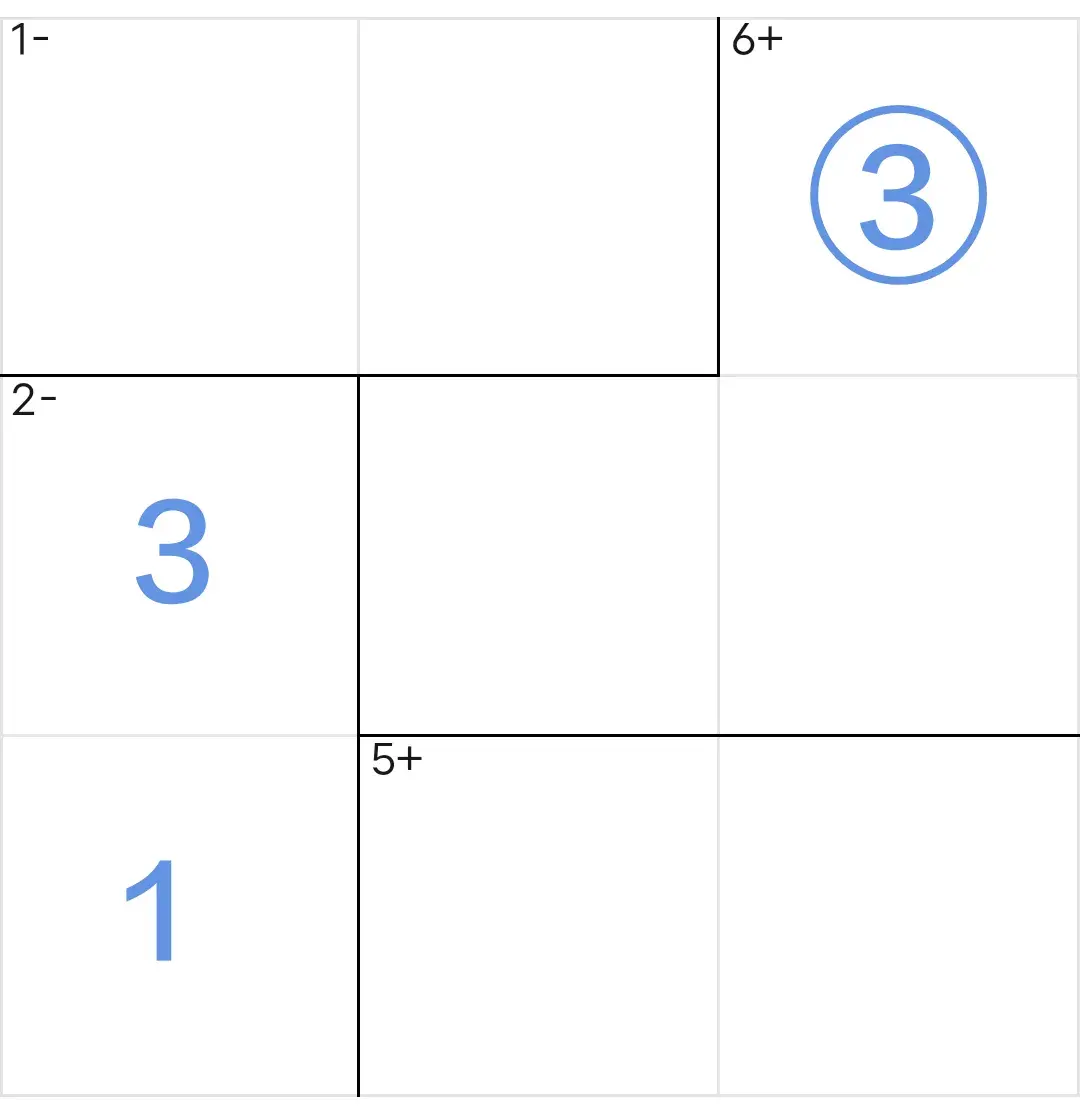
所以,r1c3=3
十,和数对法
1,和3数对法
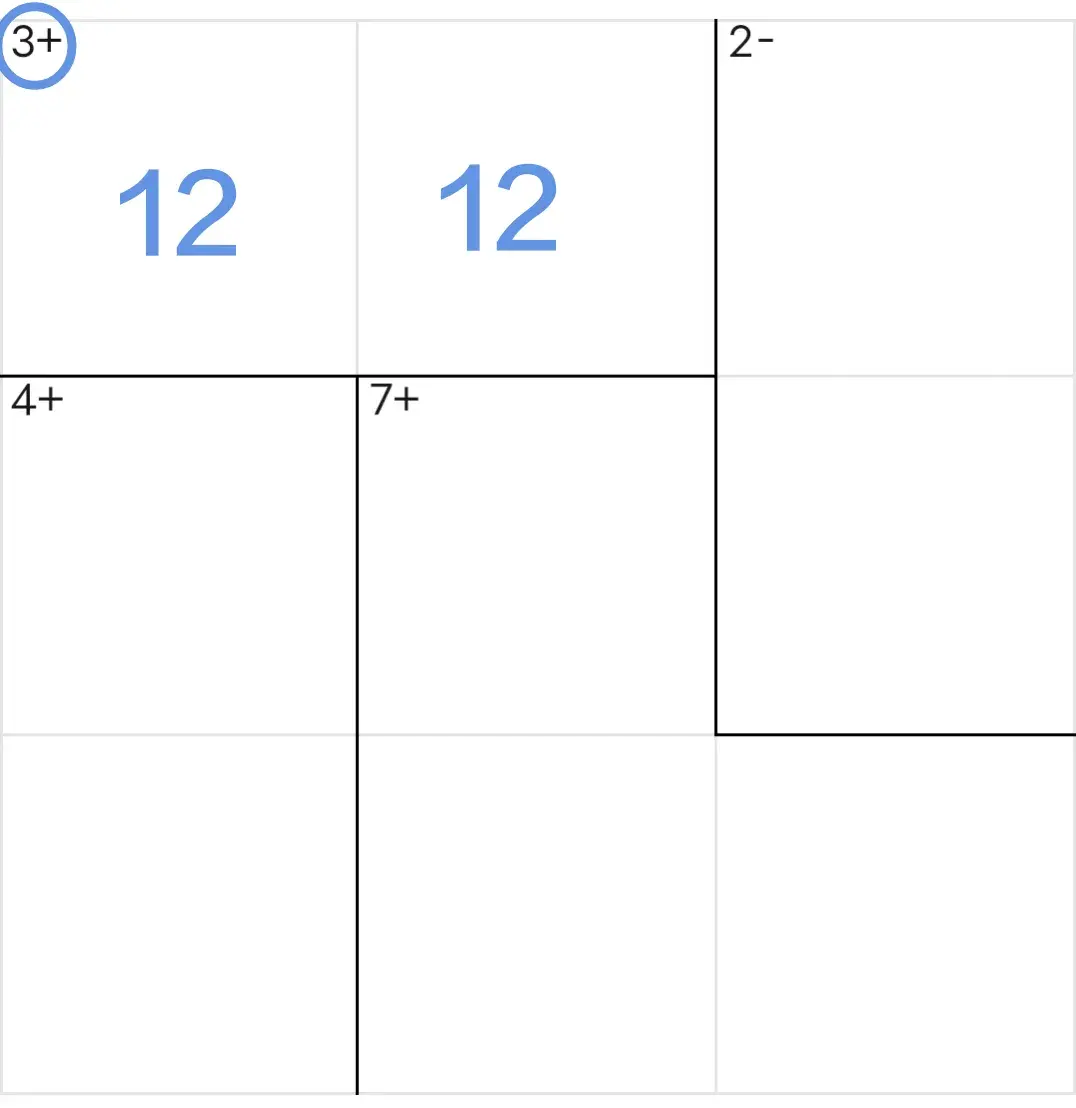
占位:数字1和2只能填入这两个单元格中,但是,具体说哪一格填1、哪一格填2还不能确定。
删除:数对所在行的其他位置中不能再有数字1和2,也就是说能够删除数对所在行的其他位置中数字1和2。
2,和4数对法
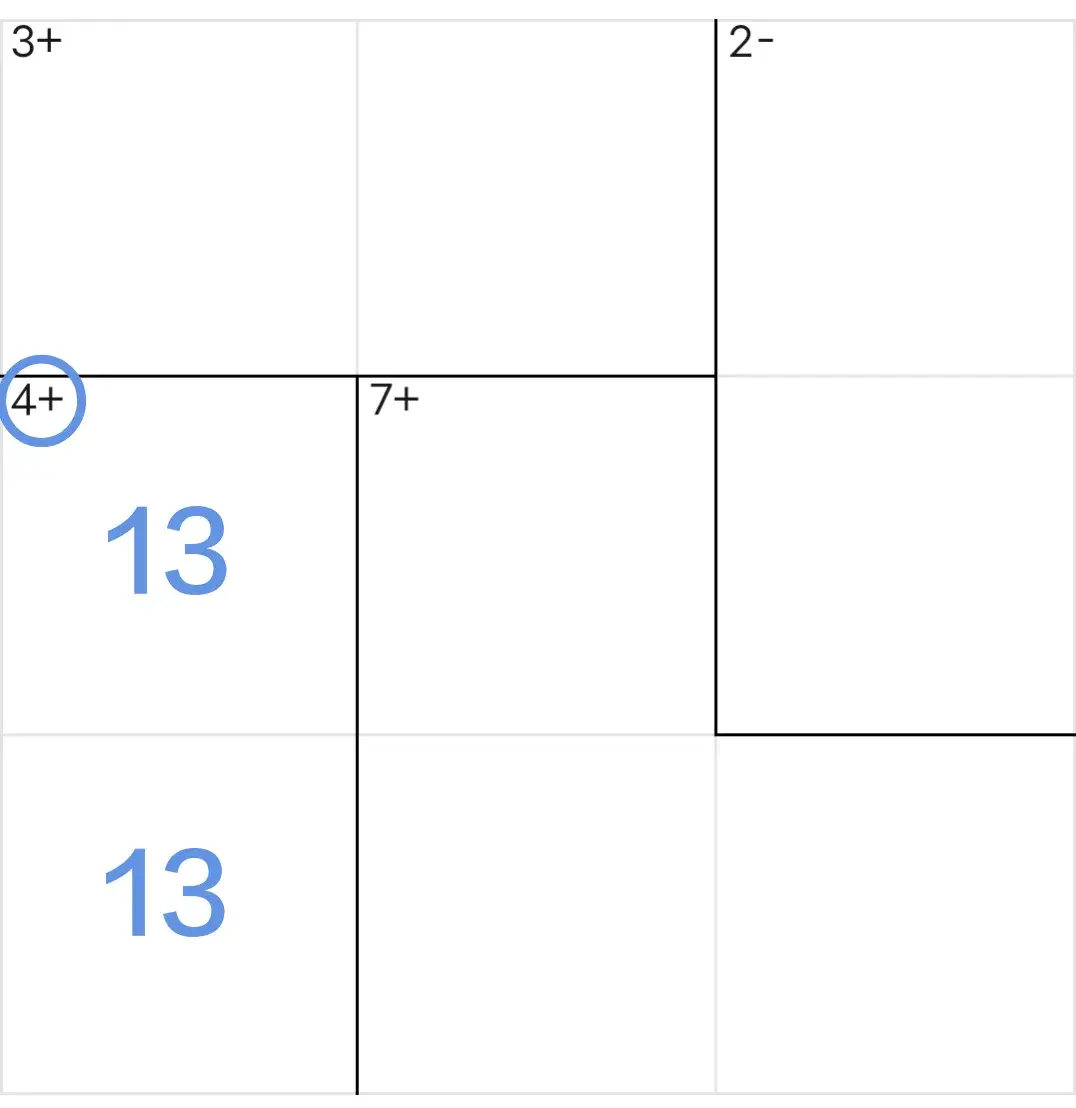
占位:数字1和3只能填入这两个单元格中,但是,具体说哪一格填1、哪一格填3还不能确定。
删除:数对所在列的其他位置中不能再有数字1和3,也就是说能够删除数对所在列的其他位置中数字1和3。
3,和5数对法
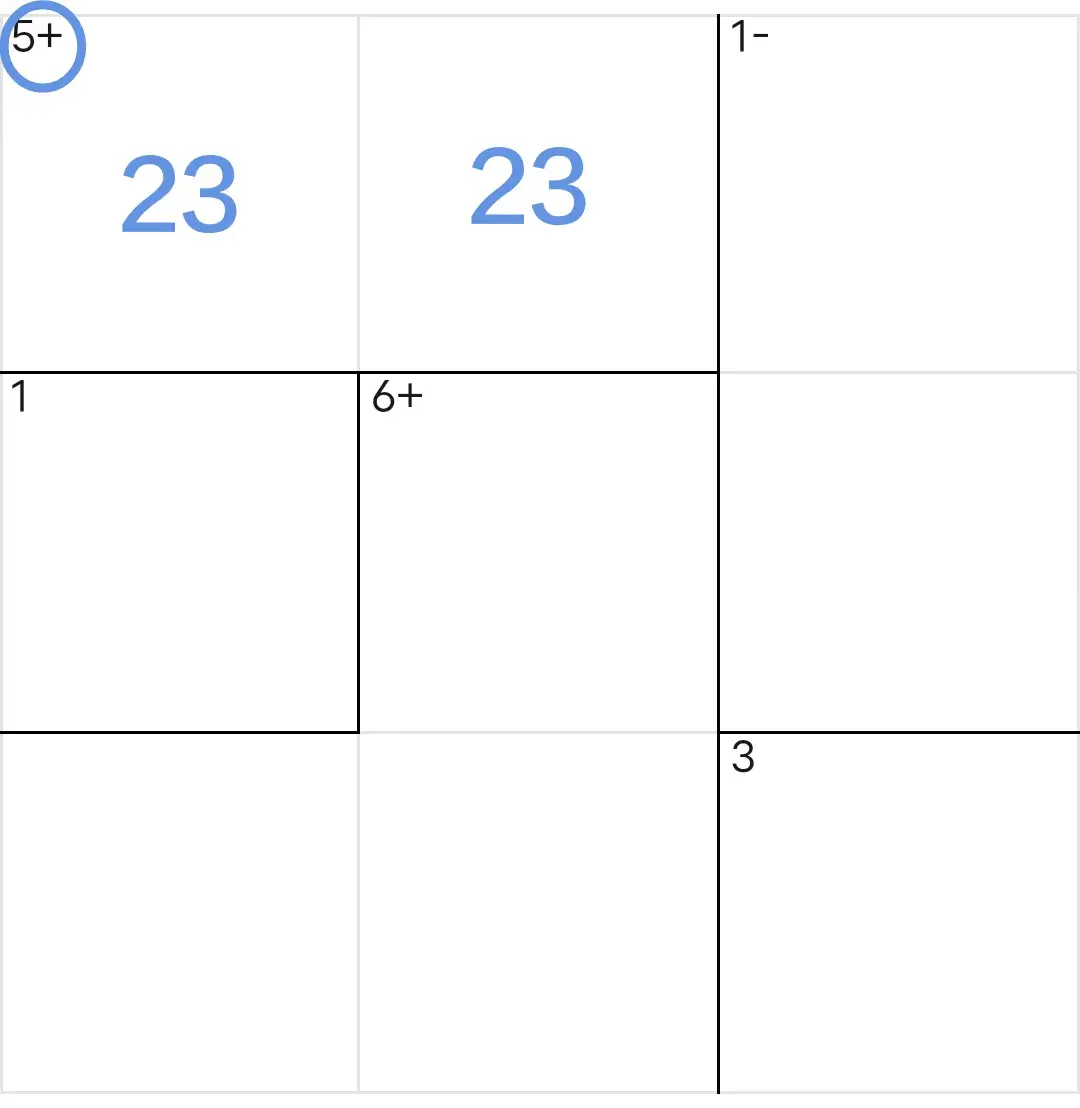
占位:数字2和3只能填入这两个单元格中,但是,具体说哪一格填2、哪一格填3还不能确定。
删除:数对所在列的其他位置中不能再有数字2和3,也就是说能够删除数对所在行的其他位置中数字2和3。
十一,差2数对法
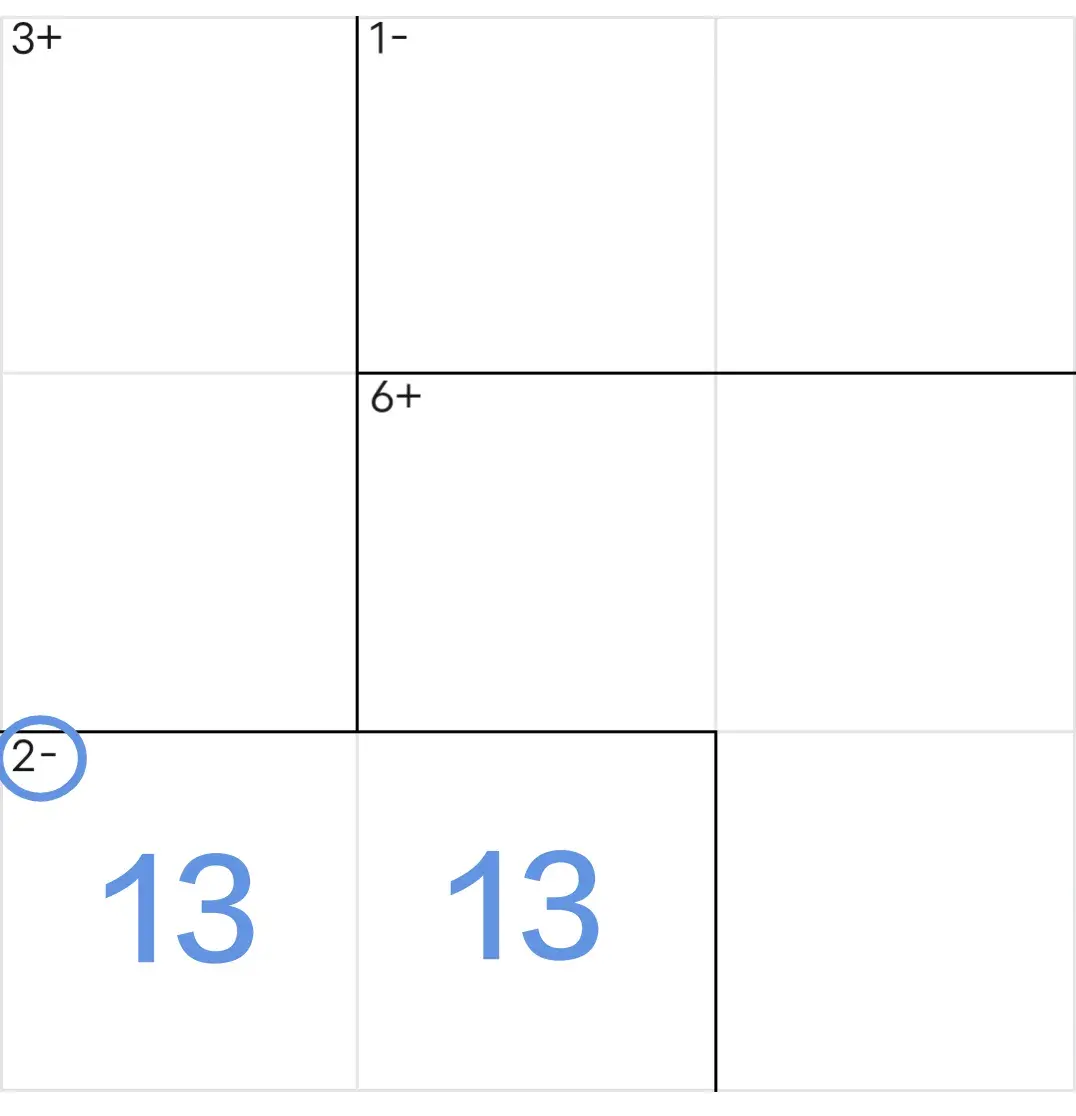
占位:数字1和3只能填入这两个单元格中,但是,具体说哪一格填2、哪一格填3还不能确定。
删除:数对所在行的其他位置中不能再有数字1和3,也就是说能够删除数对所在行的其他位置中数字2和3。
十二,积数对法
1,积2数对法
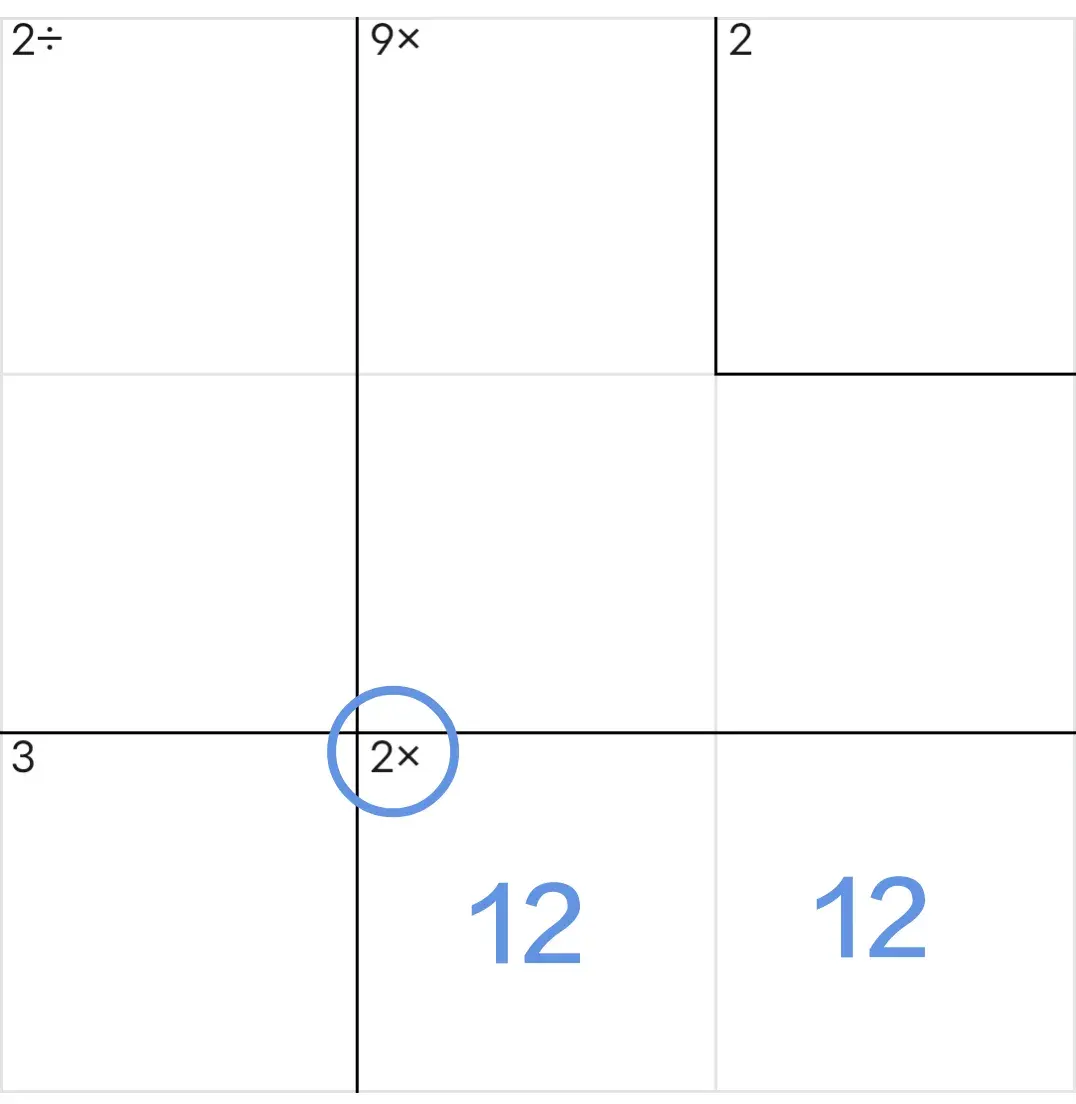
占位:数字1和2只能填入这两个单元格中,但是,具体说哪一格填1、哪一格填2还不能确定。
删除:数对所在行的其他位置中不能再有数字1和2,也就是说能够删除数对所在行的其他位置中数字1和2。
2,积3数对法
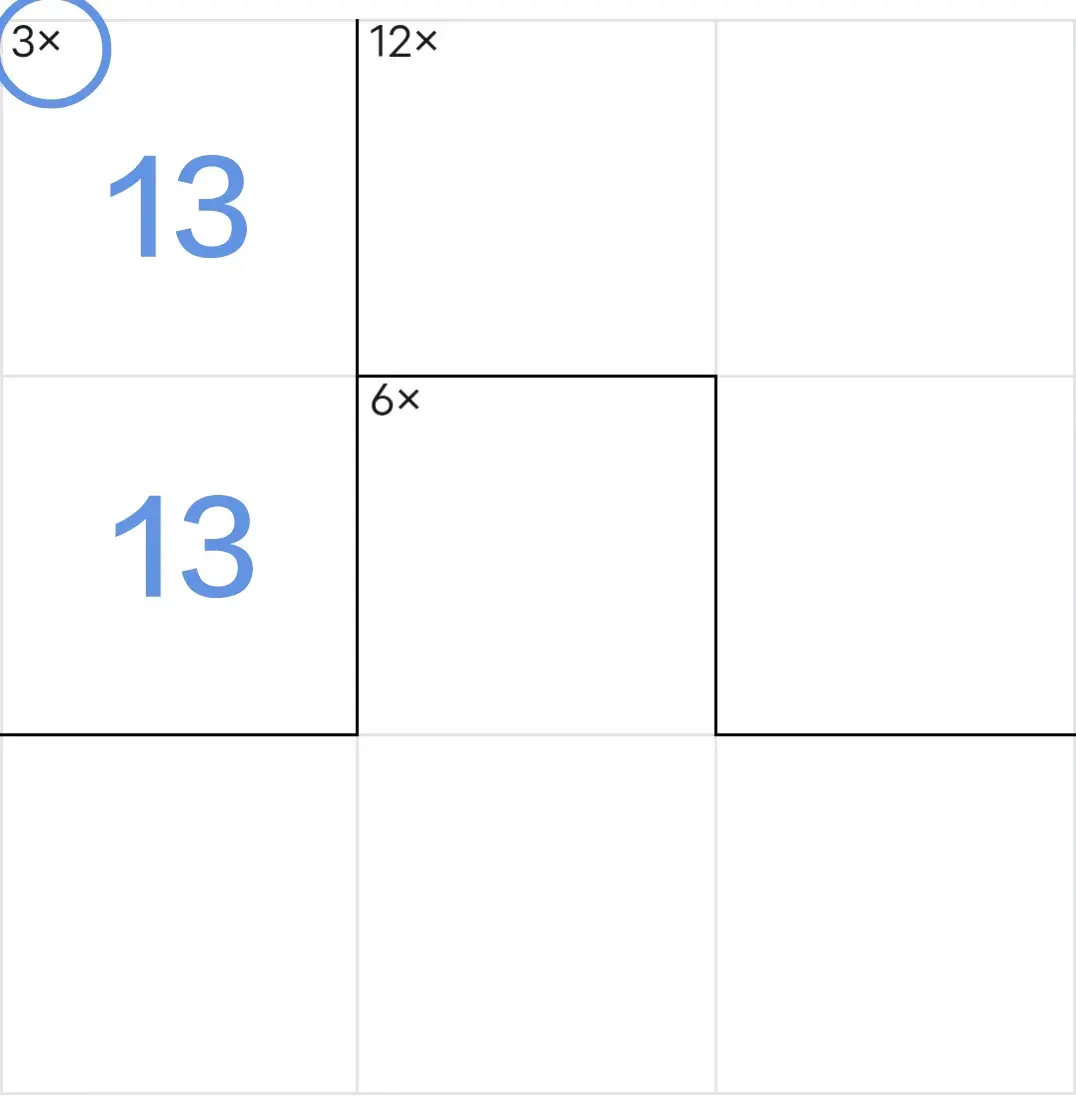
占位:数字1和3只能填入这两个单元格中,但是,具体说哪一格填1、哪一格填3还不能确定。
删除:数对所在列的其他位置中不能再有数字1和3,也就是说能够删除数对所在列的其他位置中数字1和3。
3,积6数对法
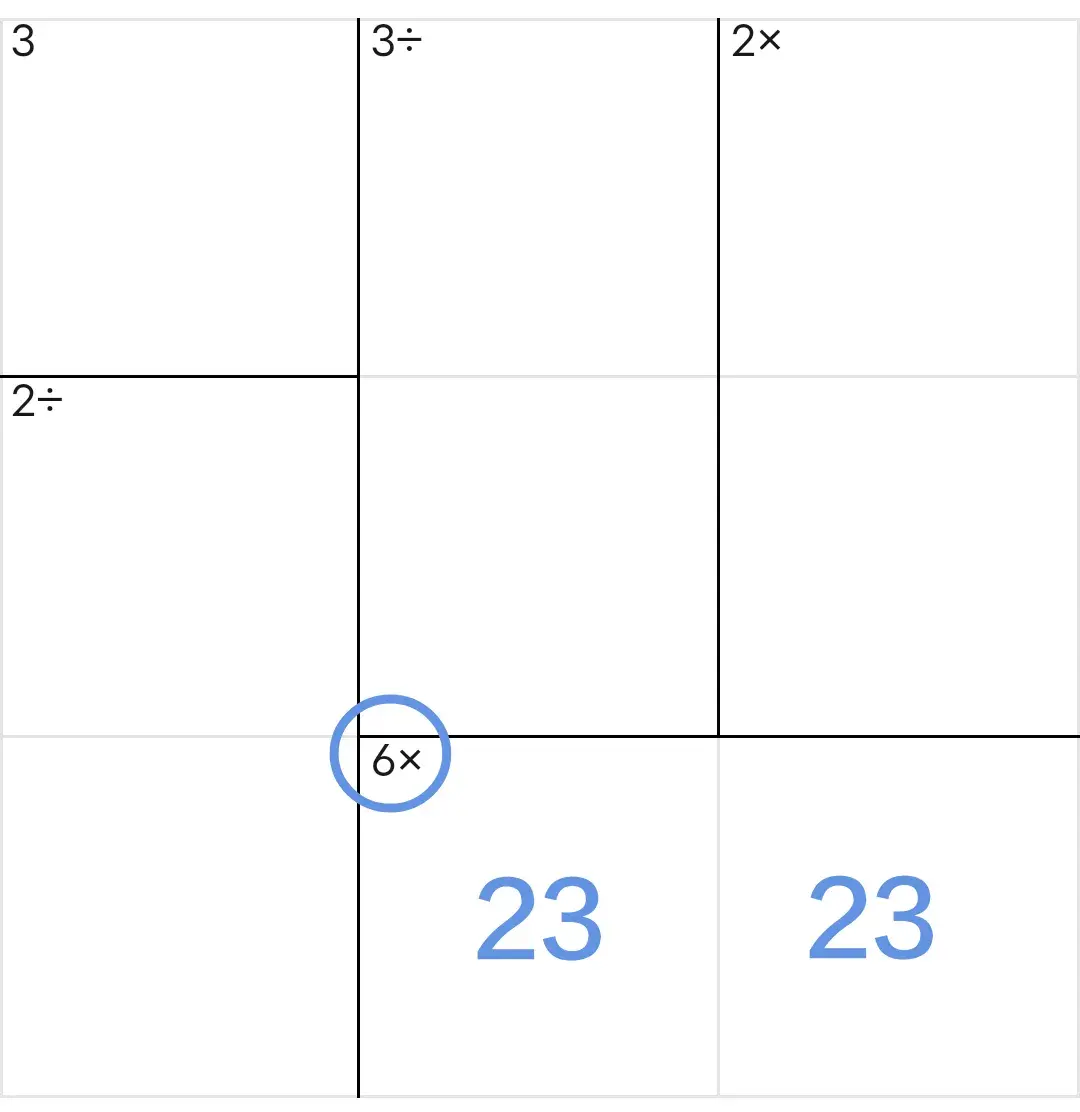
占位:数字2和3只能填入这两个单元格中,但是,具体说哪一格填2、哪一格填3还不能确定。
删除:数对所在行的其他位置中不能再有数字2和3,也就是说能够删除数对所在行的其他位置中数字2和3。
十三,商数对法
1,商2数对法

占位:数字1和2只能填入这两个单元格中,但是,具体说哪一格填1、哪一格填2还不能确定。
删除:数对所在列的其他位置中不能再有数字1和2,也就是说能够删除数对所在行的其他位置中数字1和2。
2,商3数对法

占位:数字1和3只能填入这两个单元格中,但是,具体说哪一格填1、哪一格填3还不能确定。
删除:数对所在行的其他位置中不能再有数字1和3,也就是说能够删除数对所在列的其他位置中数字1和3。