我们知道地球的极半径是6356.752千米。这个数值,并非是有了现代设备才能够计算的,而是早在两千多年前,就由古埃及科学家测量出来了。虽然并没有如今这么精确,但是其计算方法,还是令我们这些不懂数学和物理的人瞠目结舌的。那么,这位科学家是谁呢?他是如何计算出来的呢?

他叫做埃拉托色尼,他是世界上最早有文字记载的、测量出地球周长的人。而这个测量方法,其实就是简单的高中数学知识。
埃拉托斯特尼才智高超而且多才多艺,除了地理、数学,他在天文、机械、历史和哲学等领域里都有涉足,并且造诣精湛,他还是一位不错的诗人,用现在的话可以说是“文理兼修”,各方面综合素质来看,他是罕见的“奇才加全才”。不过在那个时代,他在很多领域总是排在第二位,于是有个外号“β”,那谁是第一位呢?那就是古希腊最伟大的科学家阿基米德。两人是亲密的朋友,能得到“β”外号也是一种崇高的荣誉。

埃拉托斯特尼出生于公元前3世纪的埃及亚历山大里亚城,曾应埃及国王的聘请,任皇家教师,并被任命为亚历山大里亚图书馆研究员。从公元前234年起担任图书馆馆长。当时亚历山大里亚图书馆是最高科学和知识中心,收藏了古代各种科学和文学论著。埃拉托斯特尼利用了他的职位之便,阅读了大量资料和地图。他在地理学方面的杰出贡献,集中地反映在两部代表著作中——《地球大小的修正》和《地理学概论》。前者论述了地球的形状,并以地球圆周计算为著名。他对天文学很感兴趣,崇拜希腊著名科学家亚里斯多德。亚里斯多德著有《天论》一书,他认为大地是一个球体,一部分是陆地,一部分是海洋,外面包的一层是空气。埃拉托斯特尼接受了亚里斯多德的理论,而且还想亲自量一量地球究竟有多大。当时人们都认为他是异想天开。

油画:埃拉托色尼正在教学
在古埃及,有一口井,当时非常著名,坐落于古城塞恩的尼罗河中一个河心岛洲上。每年夏至的时候,太阳光恰好在这口井的上方直射(显然,这口井正好位于北回归线)。聪明的埃拉托色尼想到,也许,太阳光是计算地球直径的最佳工具。
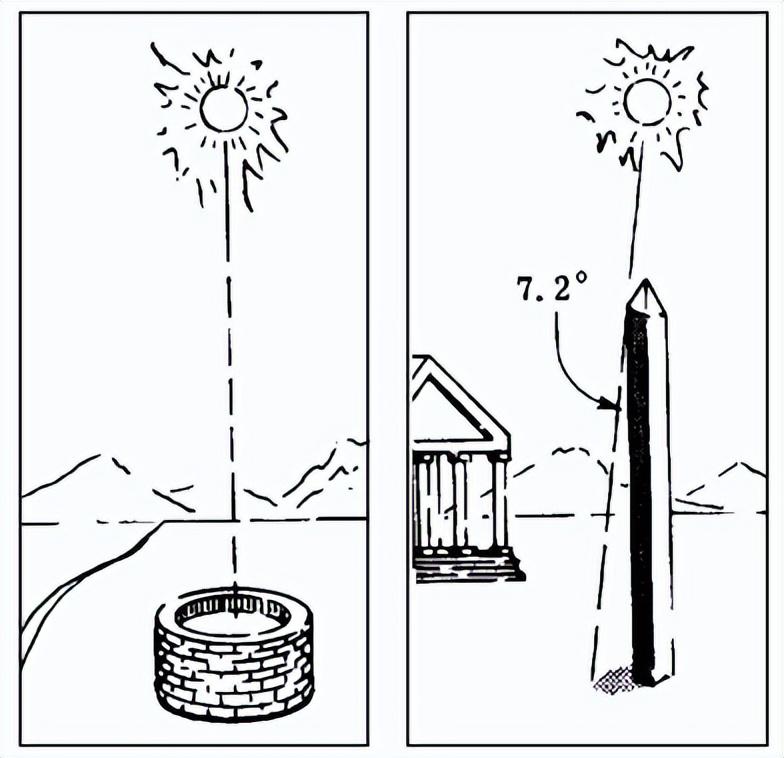
同一时间太阳光直射阿斯旺的某井,亚历山大的木杆却有阴影。埃拉托色尼就是根据这细微的不同计算了地球大小
他想了想,来到了南方的一座城市——亚历山大港。在另一年的夏至,他观察着这座城里的一座方尖塔。由于它在那口井的南方,所以夏至的时候,太阳会在方尖塔的南边塔脚投射出一个影子。通过塔的高度和影子的长度,就可以计算出太阳光与塔的夹角。
埃拉托色尼想到了一个著名的数学定理:泰勒斯的平行夹角定理。这个定理,放在现在只是初中数学知识,那就是一条直线穿过两条平行线所形成的同位角相等。在那个时候,人们认为太阳光是平行线(当然,即使在现在,由于日地距离过于遥远,太阳光也是可以被看作是平行线),因此这个定理就派上了用场。
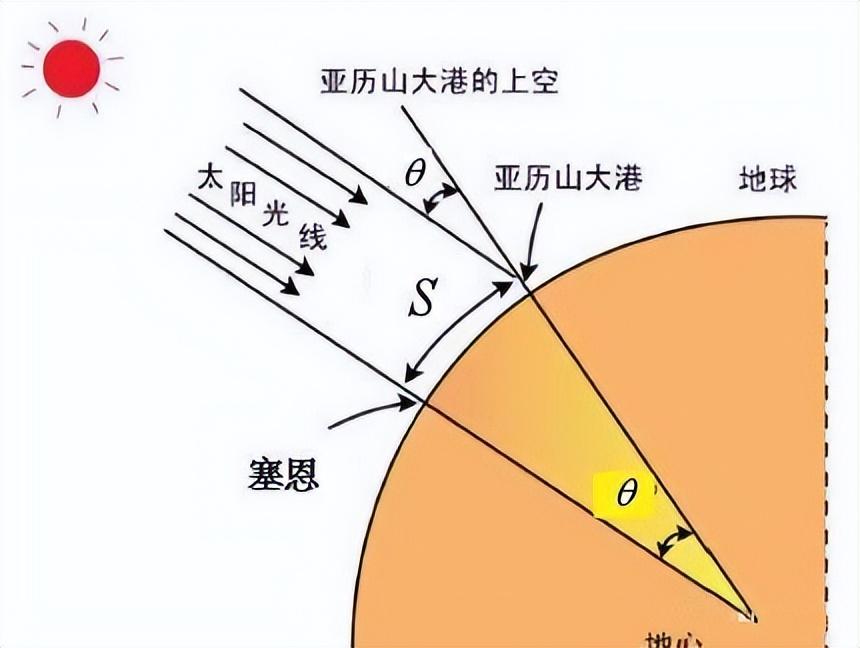
测量原理图
因此,太阳光与塔的夹角,就是两座城市分别连到地心的两个半径的夹角。根据他的测量,这个角度大约是7°12′(没错,这就是三角函数,在没有计算器的年代,人们整理了三角函数的表格,可以供他查阅)。
这个角度,大约是圆周360°的2%,所以,只要计算出两座城市之间的距离,乘以50倍,那就是地球的周长了。而这两座城市之间的距离,就简单得多了。
他跟着一个在这两座城市之间同行的骆驼队一起,计算着骆驼一共走的步数,又计算了骆驼的步幅。经过多次反复的计算,得到的结果是5000希腊里。其中,1希腊里等于157.5米。他换算到整个地球的周长,然后为了让数字能被60整除(当时人们都习惯把圆分为六十份),于是调整为252000希腊里。换算成现代数字,就是39360公里。
可以看到,这个测量原理是不是很简单,其结果和现代数字40009公里,已经非常接近了。尤其在那个年代,这个数字已经精准得令人惊讶。
埃拉托色尼还被称为“现代地理之父”!
下图就是他绘制出的世界地图,欧洲(Europe)和地中海、黑海很清晰,意大利小靴子、希腊半岛和伊比利亚半岛历历在目,英伦岛的位置也很准确,说明在那个时代,中东核心区域对于欧洲的认识已经很深入。
而非洲部分只记录了利比亚(Libya)和尼罗河上游的努比亚(Nubiana,在今天埃及南部和苏丹北部)。
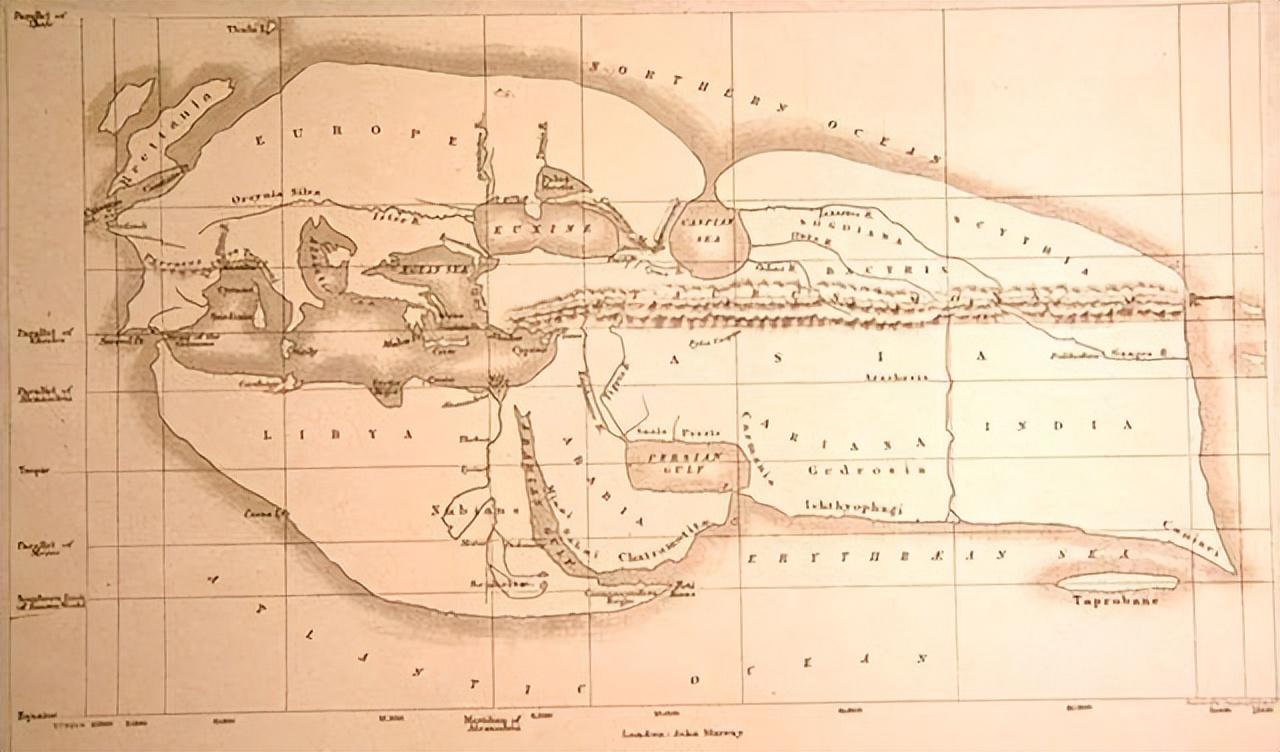
埃拉托色尼绘制的第一张“世界地图”
但如果你以为埃拉托色尼只会丈量大地,那你就大错特错了!他还把视线转向天空,他要测量月球的大小。
他的方法也很简单:仰望天空,观察月食,计算月食发生的时间。
当月球恰好从地球阴影里穿过,原本接受太阳照射的月球被地球的阴影遮挡,这就是月食。
埃拉托色尼观察了好几次月全食,发现每次月球从出现阴影到完全被覆盖,需要50分钟时间,而从月球完全被遮挡住到月球恢复完全明亮,大约需要200分钟。
由于太阳距离地球、月球很远,太阳光线可以被视为平行光,地球的阴影是一个比较标准的圆柱,月球在阴影中走的距离就等于地球的直径。
这就说明,月球的直径大约是地球的1/4。
很显然,这种假设会有一定的误差。现在测得地球的直径约为12742千米,月球直径为3476.28千米,看来,埃拉托色尼的推算结果还算是比较正确的。
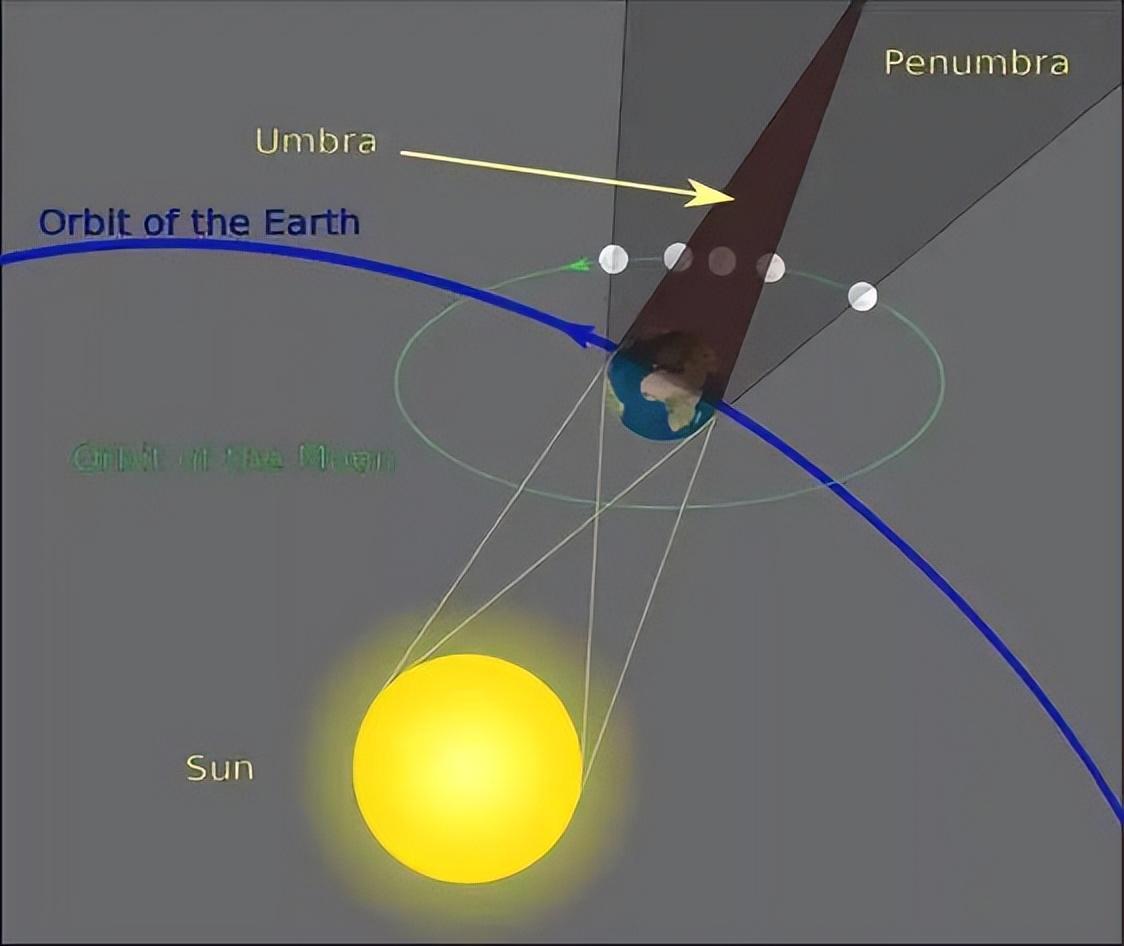
埃拉托色尼计算月球直径的示意图,但其实地球阴影有本影(Umbra)和半影(Penumbra),这种算法有微小误差
接下来,他又将自己的大拇指甲盖对准了月球,这是要做啥呢?
原来,他是想测量地月距离。他发现伸直手臂时,大拇指甲盖恰好可以覆盖月球。
他的手臂约是大拇指甲盖宽度的100倍,按照相似三角形原理,地月距离应该也是月球直径的100倍。
他给出的数字是32万公里,这和现在测得的384400公里还算得上是处于一个数量级,误差还是大了点,看来大拇指还真的是不靠谱。

埃拉托色尼用指甲盖测量月球距离
有传说,埃拉托色尼还测量了地日距离,在月相恰好为半满月时,也就是上弦月或下弦月时,他利用三角学测量地月连线和日地连线的角度,为87°(如下图,日地月的角),然后用三角函数和地月距离就能计算出日地距离为地月距离的20倍。
很可惜,当时的测量方法还是落后了点,现代人测出的角度应该是89.85°,实际上太阳比月球远400倍。
所以,更好的测量工具才会使科学家更加接近正确的答案。
有了日地距离,再用手指甲盖的方法就好测量太阳的大小了。可惜的是,一步错,步步错,错误的前提当然得不到正确的答案。
有其他说法,认为上述方法是同时期另一位科学家阿里斯塔克斯所用的,来自这位科学家的作品《关于太阳与月亮的大小和距离》。
近年来,也有人重新研究过去的文献,发现埃拉托色尼用的也许是其他方法,而他所得到的数字来自凯撒利亚的尤塞比乌斯写作的《福音论》,和正确答案也相差20倍。
但很可能是尤塞比乌斯搞错了当年的计量单位,其实埃拉托色尼计算得到的数字就是149,000,000 km,和现在的正确答案相差无几。