塞瓦定理的证明及其应用
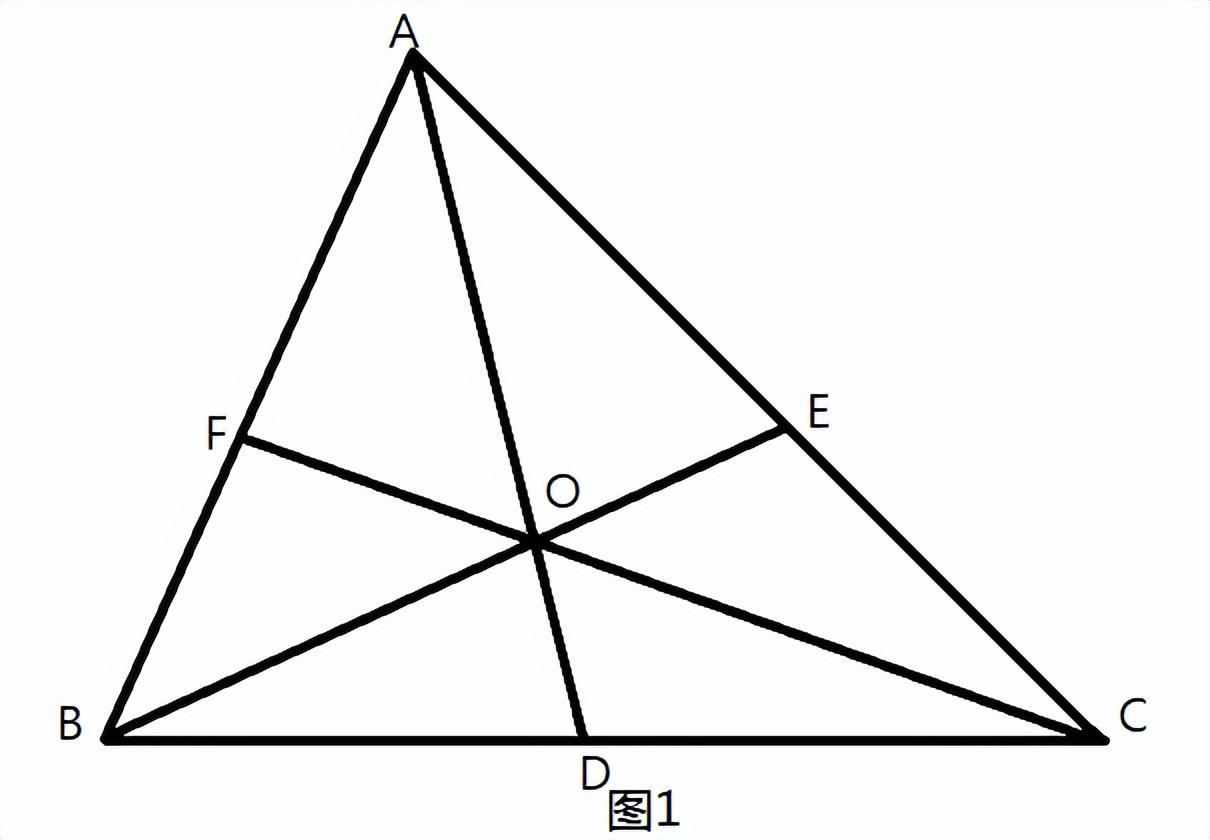
塞瓦定理是指在三角形内任取一点O(图1),延长AO、BO、CO分别交对边于D、E、F,则有
BD/DC·CE/EA·AF/FB=1。
证明方法一(面积法):
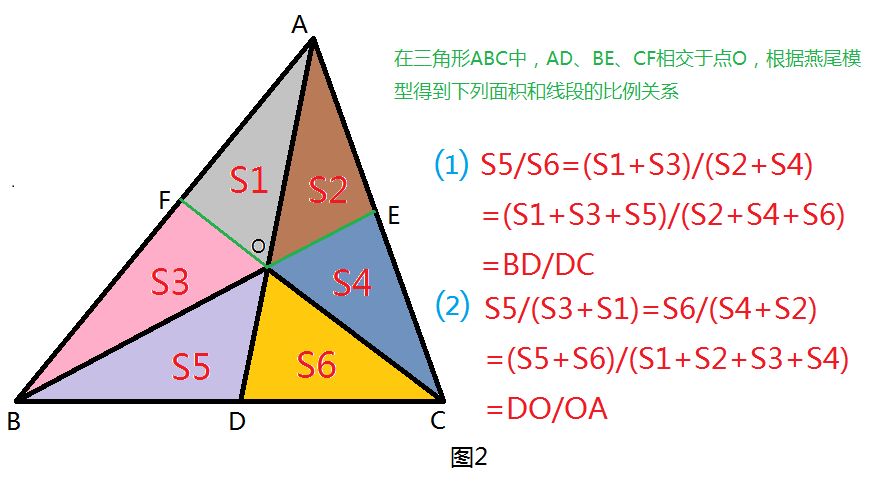
根据燕尾定理(图2)得:
BD/DC=S△ABO/S△ACO;
CE/EA= S△BCO/S△ABO;
AF/FB= S△ACO/ S△BCO。
故BD/DC·CE/EA·AF/FB
= S△ABO/S△ACO·S△BCO/S△ABO·S△ACO/ S△BCO=1。
证明方法二(平行线法):
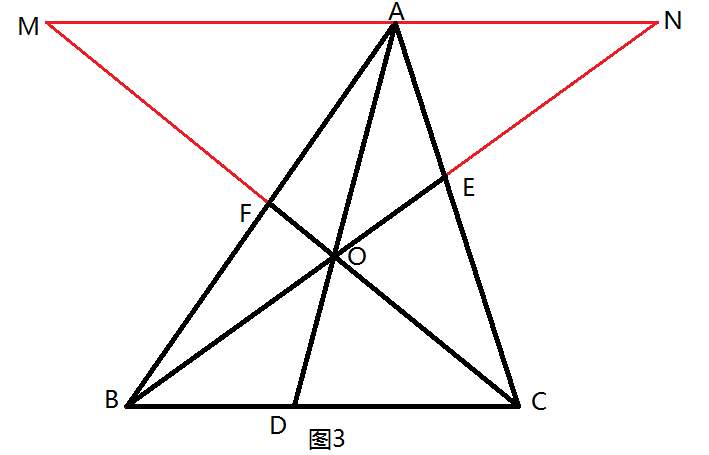
过点A作MN∥BC(图3),可得下列几组相似三角形及成比例线段:
AN/BD=AO/DO=AM/DC,即
BD/DC= AN / AM。
故BD/DC·CE/EA·AF/FB
= AN / AM·BC/AN·AM/BC
=1。
使用塞瓦定理可以进行线段长度比例的计算及线段等量关系的证明,现举例如下。
题目1:如图4,在△ABC中,点D、E、F分别在边BC、AC、AB上,AD、BE、CF相交于点O,若BD/DC=2/3,AE/CE=5/3,则AF/BF的值为(5/2)。
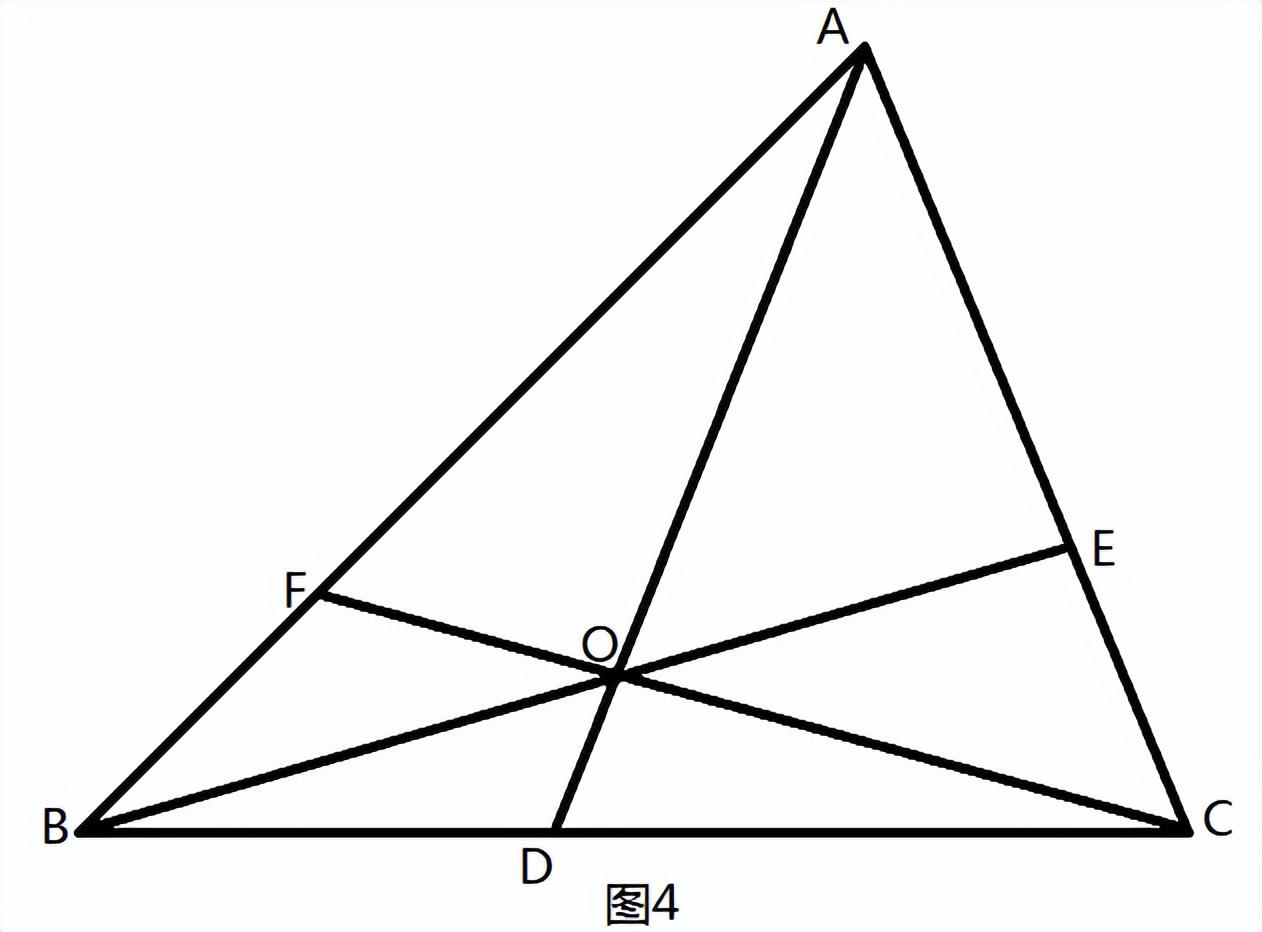
解题思路:题目已知:BD/DC=2/3,AE/CE=5/3,即CE/EA=3/5。根据塞瓦定理有:
BD/DC·CE/EA·AF/FB=1,将上述2个比值代入得:
2/3 x3/5 AF/FB=1,
AF/FB=5/2。
题目2:如图5,AD是锐角△ABC的边BC上的高,H是AD上一点,连接BH、CH并延长分别交AC、AB于E、F。求证:∠EDH=∠FDH。
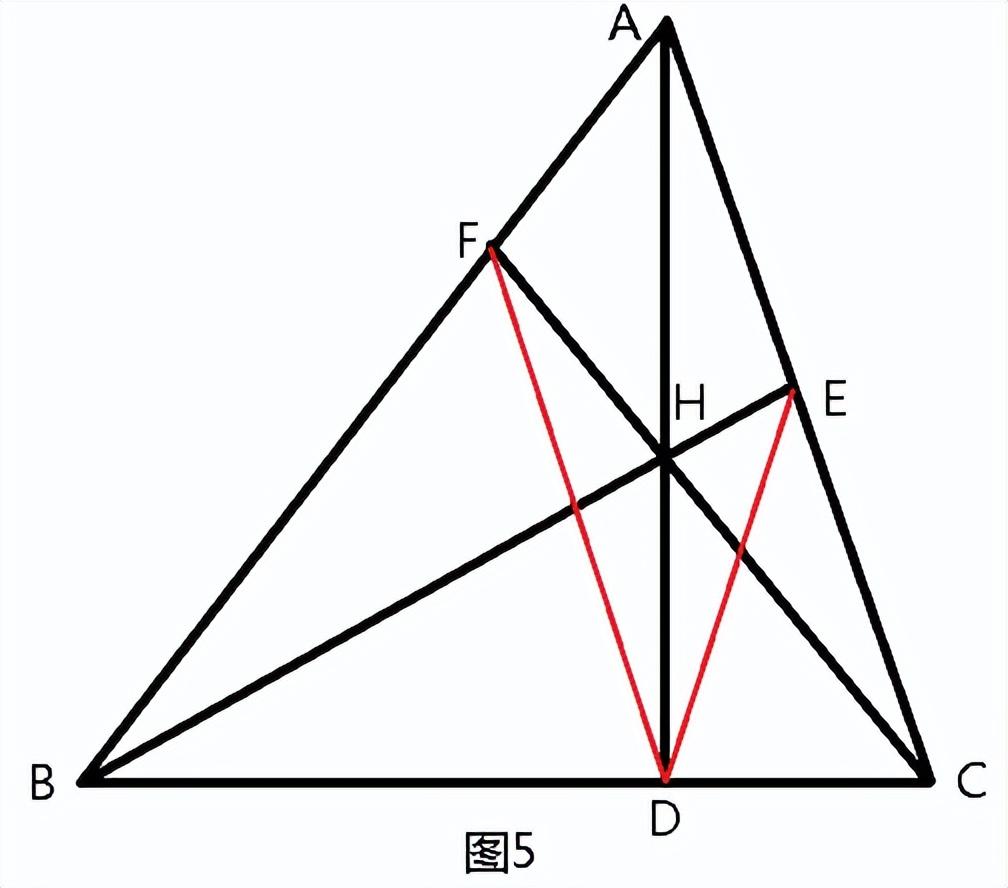
解题思路:该题含塞瓦定理的基本图形,构造平行线可出现相似三角形,且与塞瓦定理的三个关键点D、E、F一定要建立某种联系。
过A点作底边BC的平行线,延长CF、CE分别交该平行线于P、Q,显然DA⊥PQ,题目欲证∠EDH=∠FDH,即∠QDA=∠PDA,如能证明PA=AQ就大功告成。
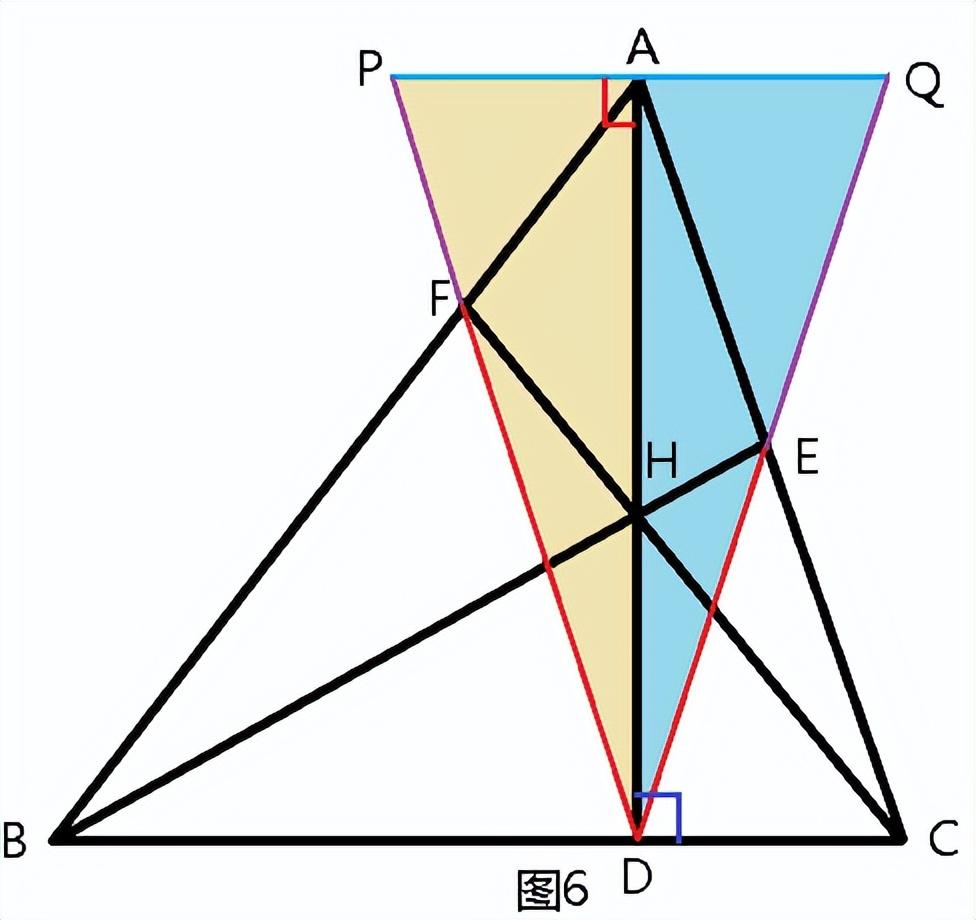
因PQ∥BC可得到2组含塞瓦定理各线段及PA、AQ的相似三角形及其线段比例关系:
PA=BD ( AF/FB);
(2) △AEQ∽△CED,AQ/DC=EA/EC,
AQ=DC (EA/EC)。
根据塞瓦定理:BD/DC·CE/EA·AF/FB=1,稍加变形得:BD ( AF/FB) =DC (EA/EC),则
PA=AQ。
易证Rt△ADP≌Rt△ADQ
故∠EDH=∠FDH成立。
该题证明方法奇妙,很有借鉴价值。