
对于中学数学所涉及的一些简单函数,求函数的值域的常用方法有好几种,本文仅介绍其中一种:反函数法。
如果函数y=f(x)的反函数y=f⁻¹(x)存在,那么函数y=f(x)的值域,就是它的反函数y=f⁻¹(x)的定义域。因此,当给定的函数的反函数易于求出时,就可借助这一关系来求出给定函数的值域。
求下图函数的值域。
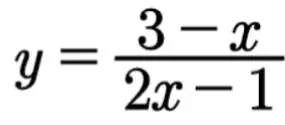
分析:求这个函数的定义域比较简单。要使函数关系式有意义,分母不能为零。所以,一眼看出这个函数的定义域。
于是问题转化为求这个函数的反函数。这也不难,解题过程请看下图:

此函数的定义域为:
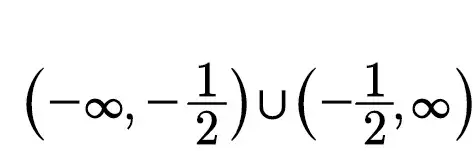
故所求函数的值域为
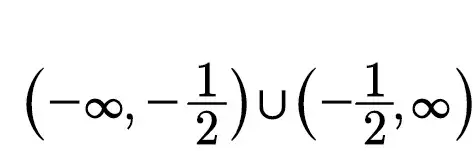
即所求函数的值域为≠-1/2的全体实数。
反函数是怎么求出来的呢?有点像解方程。如果把函数解析式看作方程,那么用含y而不含x的代数式把x表示出来,就像解方程。
求反函数比较简单,过程请看下图:

我们来看一道练习题:求函数的值域。
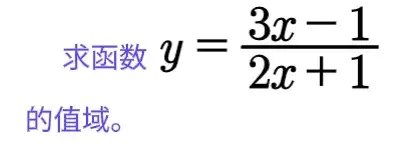
仿照例题,我们用反函数法解答这道练习题。
先求反函数。
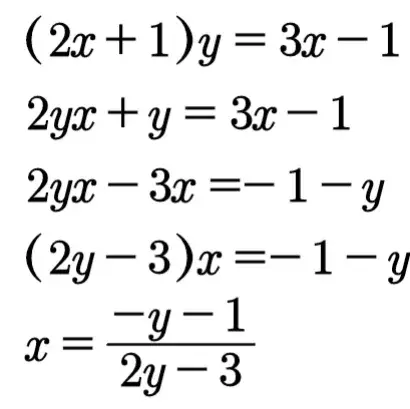
求出反函数后再求反函数的定义域。
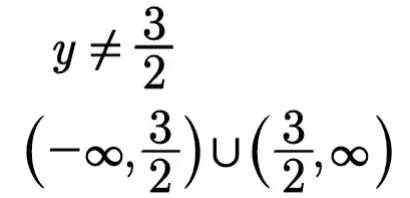
这是反函数的定义域,即所求函数的值域。
我们求出题目给定函数的反函数的定义域,从而得到了所求函数的值域。通过对以上题目的分析和解答,我们可以体会到反函数法的妙味,品味题目蕴含的数学美之对称美。