1 比较无穷大
无穷大是什么?举个直观的例子,“所有整数的数量”就是无穷大,“一条直线上所有点的数量”也是无穷大。
既然都是无穷大,那么是否意味着这两者是一样的?换句话说,我们能不能比较两个不同的“无穷大”,看看它们谁“更大”?
“所有整数的数量和一条直线上所有点的数量,这两个到底哪个大?”集合论的奠基者——著名德国数学家康托尔首次对这类看似“没有意义”的问题进行了认真的分析与解答,使人类对“无穷大”有了全新的认识。

你一定很疑惑:都是无穷大,怎么互相比较大小?对于无穷大,我们既无法描述,更无法数清。
回忆一下我们在孩童时如何比较两堆东西的数量?拿笔和本子举例,其实很简单,只要把笔和本子拿出来一对一地比较,可以在一支笔旁边放一本本子,然后在第二支笔旁边放第二本本子,周而复始……如果本子用完了,而笔还有剩余,那么我们就可以知道是笔更多。

实际上,这就是康托尔提出的比较两个“无穷大”的方法——源于人类对于物体数量最原始、最朴素的感知。我们可以将两组无穷大进行配对,每个集合里的元素分别对应另一个集合里的元素,如果它们正好一一对应,任何一个集合都没有多余的元素,那么这两个无穷大的大小相等;相对应地,如果两组无穷大无法一一对应,某个集合中存在无法配对的剩余元素,那么我们就可以说,这个集合的无穷大更大,就像我们小时候比较笔和本子的数量那样。
奇数和偶数显然都有无穷多个(这里只讨论正奇数和正偶数),用上述办法我们便可以比较它们的数量。当然,出于对数字的直觉,你肯定认为这两者是一样多的,事实上,它们也完全符合我们刚才对“一一对应”的描述:奇数和偶数可以列成一对一的组合:
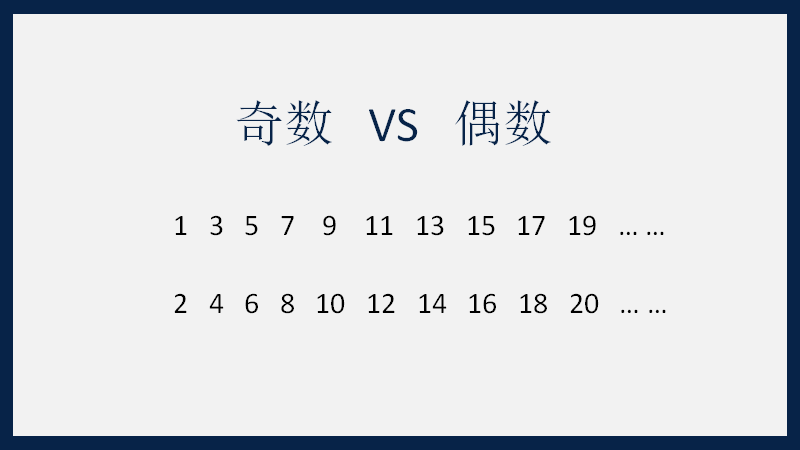
从上图中我们可以观察到,对于任意一个奇数,都有唯一对应的偶数,反之亦然。因此,奇数的数量和偶数的数量是两个相等的无穷大,这并不难理解。
换一个问题:全体正整数的数量和偶数的数量谁更大?
你也许会说:那还用说,肯定是所有正整数的数量更大,因为除了偶数以外,它还包含了奇数。但是,这只是你的直觉,令人震惊的是,如果我们依然严格按照上述方法来比较这两个无穷大,你会发现你的直觉错了,事实上所有正整数和偶数的数量竟然是一样多的!因为所有正整数的集合和只有偶数的集合也能形成一一对应:
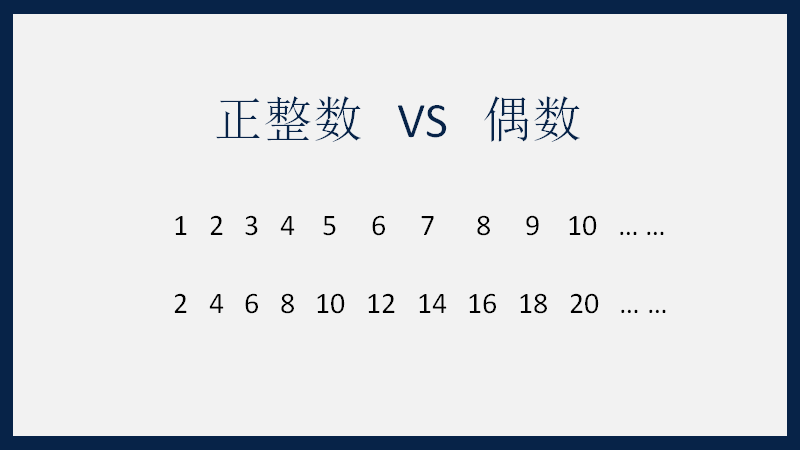
这看起来似乎很矛盾,因为偶数显然是正整数的一部分,但是请记住,我们是在讨论无穷大,在“无穷”的世界里,部分可能“等于”整体!
无穷大的诸多特性是奇特且古怪的,我们必须做好直面它们的准备。
对于“无穷大”的讨论,最有趣的例子莫过于德国数学家大卫·希尔伯特在谈到“无限大数”的奇怪而美妙的性质时提出的著名的“希尔伯特旅馆”。

我们设想有一家旅馆,内设有限个房间,而所有的房间都已客满。这时来了一位新住客,想订个房间,“对不起”,旅馆主人说,“所有的房间都住满了。”
再设想另一家旅馆,内设无穷多个房间,所有的房间也都客满了。这时也有一位新住客,想订个房间。
“不成问题!”旅馆主人说。接着他就把1号房间的旅客移到2号房间,2号房间的旅客移到3号房间,3号房间的旅客移到4号房间等等,这样继续移下去。这样一来,新住客就被安排住进了已被腾空的1号房间。
现在我们继续想象,一家旅馆拥有无穷多个房间,现在来了无穷多个新住客。
“没问题,先生们,请等一会儿。”旅馆主人说。
他把1号房间的旅客移到2号房间,2号房间的旅客移到4号房间,3号房间的旅客移到6号房间,如此进行下去……
这样的话所有奇数号的房间都空出来了,无穷多位客人轻轻松松就安置了下来。
这个“反直觉”的故事巧妙地揭示了“无穷大数”不同于普通数字的奇妙特性。
根据康托尔的“无穷大比较法则”,我们现在还能证明有理数的数量等于整数的数量。
稠密的有理数集与疏散的它的整数子集的元素一样多,乍一看这似乎不可理喻,因为我们不能像罗列奇数、偶数、整数那样把有理数一个个从小到大罗列出来(因为任意给定的两个有理数之间存在无穷多个有理数)。但是别忘了,在无穷的世界中,什么都有可能发生!来试试看吧。
我们知道一个有理数总能写成的形式,接下来我们可以制作一张表格,使某个有理数在这张表格的第列第行,例如把放在下面表格中的第3列第4行:
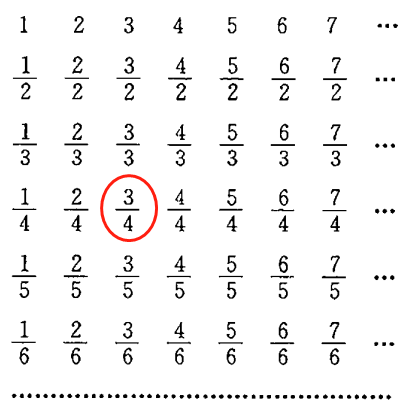
现在所有的(正)有理数便都可以放进这张由无穷多个元素组成的表格中,接着我们画一条连续的折线去通过表格中所有的数,如下图所示:
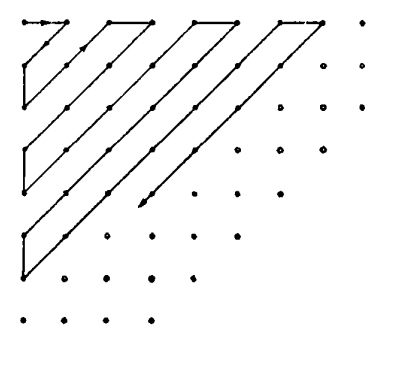
沿着这条折线走,我们便可以遍历所有的(正)有理数,得到一个序列,在这个序列中我们可以把相同的数删去(如等等),使得每一个有理数以最简单的方式恰好出现一次,因而得到一个全新的序列其中每一个正有理数有且只出现一次,这便说明全体有理数是可数的,它可以和正整数形成一一对应。因此我们便可以知道:整数的数量实际上和有理数的数量是一样多的。
你可能猜想:既然已经比较了那么多种无穷大且发现它们都是可以一一对应的,那是否意味着所有的无穷大都是一样的呢?
事实上情况远非如此,康托尔通过缜密的分析发现了一个惊人的事实:全体实数集是不可数的,换句话说,全体实数与整数或有理数相比有根本的不同,可以说,它是更高级的“无穷大”。关于这个事实康托尔用反证法给出了一个天才般的证明:
假如有人宣称他能完成实数与整数的一一对应,那他应该罗列出这样的对应关系
其中这些表示整数部分,小写的字母表示小数点后的数码,假设这个序列包含了所有实数(当然,我们不可能真的写出无穷多个无限小数的每一位数,那么这张表的作者必然有自己的一套排列法则,就像我们之前排列有理数那样)。
实际上,不难证明,任何排列法则都保证不了这样的事情,因为我们随时可以写出一个无限小数,它绝对不可能属于这张没有尽头的表。
怎么办到?很简单,首先选取一个数码不同于,选取一个数码不同于,同样地,不同于等等……现在考虑无限小数
这个新的数一定不等于上表中的任意一个数,因为它的第个数码和表格中的第个数不同,这便说明实数集是不可罗列的。
由于实数与数轴(直线)上的点一一对应,因此我们便可以回答本文一开始提出的问题:所有整数的数量和一条直线上所有点的数量,显然是后者更大。
直观上来看,你也许会认为有限长的线段上点的数量一定远小于无限长的直线上点的数量,但是事实并非如此!如果我们在一条线段的和处将其折弯,再从一点投影(如下图),由此可知,即使是有限长的线段,也一一对应了无限长的直线上的无限多个点。
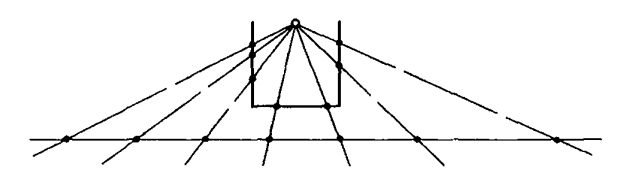
同样地,另一个看似显然的事实往往也是错误的:一个二维的正方形肯定比一维的线段包含有“更多”的点。事实上,它们的数量应该相等。为了证明这一点,我们可以考虑将正方形放入平面直角坐标系中去。
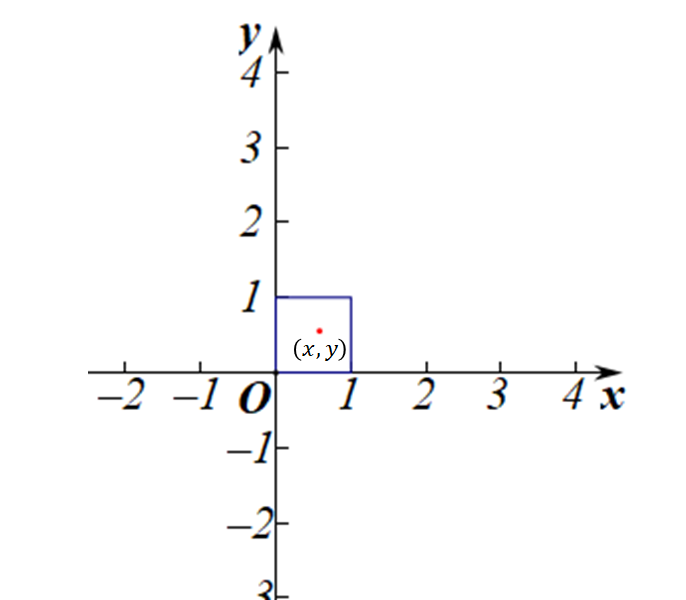
如果点是单位正方形中的点,假设其坐标可以写成十进位小数的形式:
那么我们可以将其唯一对应到数轴上从0到1这个线段上的一点,这便说明正方形上的点和线段上的点是一样多的。
类似地还可以证明:立方体内的点和线段上的点也是一样多的。
无穷数学的奠基者康托尔提出:如果两个无穷集合可以一一对应,那么就称其是等势的,且它们有相同的基数,我们可以用希伯来字母(alehp,读作阿列夫)来描述基数的大小,字母右下方的角标代表“无穷大”的“等级”:
现在我们可以说:整数的数量是,一条线段上点的数量是,就像平时我们说:嘿,这有3个苹果,那有2支笔这么简单。
事实上,数学家发现,几何曲线的种类大于实数的数量,因此我们可以用描述几何曲线的所有种类。正如人类在浩瀚的宇宙面前惊叹于自己的渺小,在数学中,也有比无穷大更大的无穷大,真是令人感到惊异。
